Pentominos

Pentominoes.
Pentominoes are configuration patterns made up of 5 cells which are always connected to each other either horizontally or vertically. There are 12 pentominoes which are all illustrated in the box below:
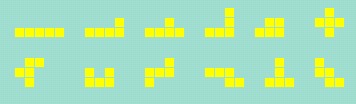
Find out the evolution of each of the patterns, except for the first pattern on the second line which we will look at later on. You should find that five of them disappear very quickly, two soon reach a stable pattern and four become traffic lights after a short time.

The only whose behaviour is of special interest is the one known as the R PENTONIMO. Conway himself studied its evolution and said the following about this pentomino: "It has left a lot of miscellaneous junk stagnating around, and has only a few small active regions, so it is not at all obvious that it will continue indefinitely." Click on the animate button in the following window to follow the evolution of the R pentomino.

If you didn't have enough patience to watch the complete evolution of the R pentomino let us explain what happens. After 1103 generations it becomes an oscillating pattern. During its evolution it produces 6 gliders travelling outwards. The junk that is left consists of four blinkers, one boat, one ship, one loaf, four beehives and eight blocks.
In our mini-world the result above depends on the initial position of the R pentomino in this world. With the position we have selected, the population becomes stable after 1226 generations.

	José Luis Alonso Borrego.

	Spanish Ministry of Education. Year 2001

Except where otherwise noted, this work is licensed under a Creative Common License