Título de la página

	ECUACIÓN GENERAL
	Geometría

1. PROGRESANDO EN EL CONOCIMIENTO DE LA CIRCUNFERENCIA
Si en la ecuación (x-h)²+(y-k)²=r² desarrollamos los paréntesis y pasamos todo al primer miembro nos queda: x²+y²-2hx-2ky+h²+k²-r²=0, esto nos sugiere que toda ecuación de la forma: x²+y²+dx+ey+f=0 será la de una circunferencia de centro h=-d/2, k=-e/2 y radio tal que r²=(d²/4+e²/4)-f. Por lo tanto siempre que d²+e²-4f>0 tendremos que la ecuación: x²+y²+dx+ey+f=0 es la ecuación de una circunferencia. Observación: Las ecuaciones de la forma ax²+ay²+mx+ny+p=0 tienen las mismas soluciones que las que resultan al dividir por a ; es decir, las de la forma x²+y²+dx+ey+f=0. Por lo tanto cada circunferencia ax²+ay²+mx+ny+p=0 también se puede escribir en la forma x²+y²+dx+ey+f=0 resultando realmente una circunferencia cuando m²+n²-pa>0 El siguiente applet nos permite modificar los parámetros d,e y f y ver el dibujo de la circunferencia correspondiente. Evidentemente los tres parámetros deben respetar siempre la condición: d²+e²-4f>0
	14.- Cambia los valores de d,e y f para obtener: - Una circunferencia centrada en el origen de coordenadas. - Una circunferencia con centro en d(3,0). - Una circunferencia con centro en (0,-2). 15.- Si el centro está en el eje de las X ¿qué parámetro se hace cero en la ecuación general?, ¿Y cuando el centro está sobre el eje Y?. Comprueba tus hipótesis dibujando varias circunferencias.
16.- Modifica los parámetros para obtener circunferencias que pasen por el origen de coordenadas. ¿Qué característica tienen las ecuaciones de las circunferencias que pasan por el origen?.

2. CIRCUNFERENCIA QUE PASA POR TRES PUNTOS
Si consideramos dos puntos A y B resulta que hay infinitas circunferencias que pasan por ellos, basta considerar la mediatriz del segmento que los une y observar que las circunferencias con centro en esa mediatriz y que pasen por uno de los puntos también pasarán por el otro.
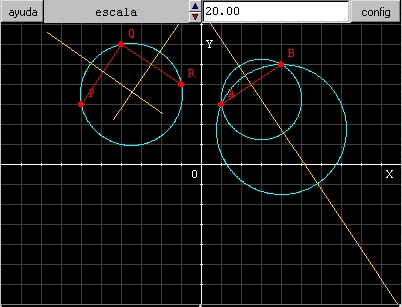	Cuando disponemos de tres puntos P, Q y R que no estén alineados, la mediatriz de PQ y la Mediatriz de QR se cortarán en un punto, ese punto es el centro de la circunferencia que pasa por P, Q y R puesto que los tres equidistan de él. Ver ilustración. Cuando los tres puntos estén alineados las mediatrices serán paralelas y no podremos encontrar un punto que equidiste de los tres.
La figura muestra como se obtiene el centro de la circunferencia que pasa por tres puntos no alineados. También observamos que por dos puntos siempre podemos hacer que pasen infinitas circunferencias.

3. CONSIGUE QUE LA CIRCUNFERENCIA PASE POR LOS TRES PUNTOS

Ya hemos comentado que cuando los tres puntos están alineados no podemos encontrar una circunferencia que pase por los tres, pero que en los demás casos sí. En el gráfico aparecen datos suficientes para conseguir mediante "ciertos cálculos" los valores de h, k y r convenientes

23.- Escribe los valores de los parámetros de la circunferencia que pasa por los puntos P, Q y R. Seguramente necesitarás hacer algunos cálculos en tu cuaderno.

En la ecuación que aparece en la parte inferior debes sustituir h, k y r por los valores obtenidos y después pulsar intro. Para obtener otra colocación de los puntos pulsa el botón inicio.

Si no aciertas a la primera puedes volver a intentarlo con nuevos valores, haz bien los cálculos.

Procura no cambiar la estructura de la ecuación de la circunferencia, porque entonces obtendrás otro tipo de curva.

	Jesús Fernández Martín de los Santos

	Ministerio de Educación, Cultura y Deporte. Año 2001

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.