|
|
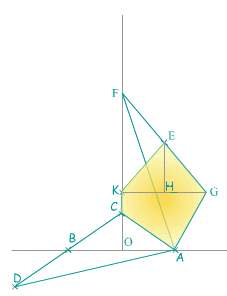
Los pentágonos teseladores (1)
|
Para
aprovechar al máximo esta página presiona la tecla
F11
![]()
Sonido
Si
los botones no actúan telecargar aquí la versión
Flash
5.