

TRES BANDAS
¿Encontraste soluciones?
![]()
1.- La primera solución la obtendremos con un rebote: "abajo-arriba-abajo".
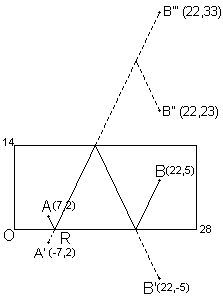
Obtenemos los puntos simétricos de A y B respecto de la banda inferior: A' y B'; y el punto simétrico de A' respecto de la banda superior: B'''. La solución será la intersección con la banda inferior de la recta que une A' y B'''.
Sol: R = "35x-15y=275" ![]() "y=0" =
(55/7,0)
"y=0" =
(55/7,0) ![]() (7'857,0)
(7'857,0)
2.- Otra solución: rebote "abajo-arriba-derecha".
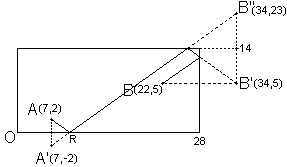
Sol: R = "25x+27y=229" ![]() "y=0" =
(229/25,0)
"y=0" =
(229/25,0) ![]() (9'16,0)
(9'16,0)
3.- Otra posibilidad: rebote "abajo-derecha-arriba".
|
Aquí: B' es el simétrico de B respecto de
la banda superior y B" su simétrico respecto de la banda derecha. R = intersección de la banda inferior con la recta que une A' y B". |
| Pero con los datos de nuestro ejemplo, el punto B" coincide con el del caso anterior y esta solución no es posible ya que la bola rebotaría antes en la banda superior que en la derecha. | 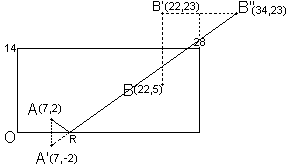 |
4.- ¿La última?: rebote "abajo-derecha-izquierda".

A' = simétrico de A respecto de la banda inferior;
B' = simétrico de B respecto de la banda izquierda;
B" =simétrico de B" respecto de la banda derecha.
R = intersección de la banda inferior con la recta que une A' y B".
Sol: R = "7x+71y=191" ![]() "y=0" =
(191/7,0)
"y=0" =
(191/7,0) ![]() (27'28,0)
(27'28,0)
5.- ¿Y "abajo-izquierda-arriba?".
Queda como ejercicio su estudio.
Autor: Andrés Mateos Royo
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||