

Dado un triángulo ABC cualquiera, calculamos:
CASO I |
Medianas |
CASO II |
|
CASO III |
|
CASO IV |
La Mediatriz de un lado de un triángulo, es la recta perpendicular en el punto medio. También se puede estudiar como el lugar geométrico de los puntos del plano que equidistan de los extremos del segmento.
| Sea el triángulo ABC: | |||
| Vértices: | A(A.x,A.y) | B(B.x,B.y) | C(C.x,C.y) |
Posiciona el triángulo en el plano cartesiano, utilizando la escena:
Cálculo de la mediatriz:
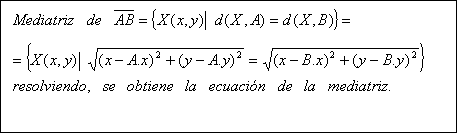
De otro modo:

| Coordenadas del punto medio de AB | |
| Pendiente de AB | |
| Pendiente de la recta perpendicular a AB | 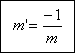 |
| Ec de la mediatriz, recta que pasa por M y de pendiente m' |
EJERCICIOS
1.- Halla las coordenadas de los puntos medios de los lados del triángulo de vértices A(2,-1), B(-4,3) y C(0,4)
2.-Calcula las pendientes de las rectas que contienen a los lados y las de sus respectivas perpendiculares.
3.- Calcula las ecuaciones de las mediatrices por los dos métodos reseñados anteriormente y comprueba que los resultados son idénticos.
4.- Calcula el Circuncentro, como punto de intersección de las mediatrices (resolviendo, el sistema determinado con dos mediatrices), comprueba tu resultado haciendo clic con el ratón sobre la escena y en el punto donde se cortan las mediatrices.
Autora: Mª del Carmen Herrero de Evan
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||