
En las páginas anteriores nos hemos interesado por el comportamiento de una determinada función en las cercanías de un punto. En esta página y en las siguientes nos interesaremos por el comportamiento de la función cuando la variable independiente, x, se hace muy grande (tiende a más infinito) o muy pequeña (tiende a menos infinito).
Conviene aquí recordar de nuevo que en los casos en los que decimos que el límite es más infinito o menos infinito, tampoco existe el límite. Decir que el límite es más infinito o menos infinito es una manera sencilla de indicar un comportamiento específico de la función, pero en ningún caso debe pensarse que las expresiones "más infinito" y "menos infinito" representan cantidades numéricas con las que se puede operar.
A continuación vamos a describir las distintas posibilidades de comportamiento de una función en el infinito, indicando la notación habitual en Matemáticas para referirse a ellas.
En cada uno de esos casos hay cuatro posibilidades:
Los valores de la función f(x) se aproximan a un cierto número real, b, cuando la variable independiente tiende a más infinito (o a menos infinito).
Desplaza la x hacia la derecha (o hacia la izquierda) en la imagen siguiente, tanto como quieras (cambia los valores de O.x para poder visualizarlo correctamente) y comprueba cómo f(x) se aproxima a b (línea verde).
Expresaremos este hecho mediante las siguientes expresiones:
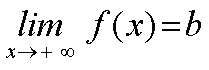 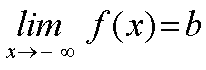
Y diremos que b es el límite de f(x) cuando x tiende a más infinito (o a menos infinito, respectivamente). Diremos, además, que la recta y=b es una asíntota horizontal de la función y=f(x). |
Los valores de la función f(x) crecen indefinidamente cuando la variable independiente tiende a más infinito (o a menos infinito).
Desplaza la x hacia la derecha (o hacia la izquierda) en la imagen siguiente, tanto como quieras (cambia los valores de O.x para poder visualizarlo correctamente) y comprueba cómo f(x) se hace tan grande como se quiera (línea verde). Desplaza hacia arriba la gráfica y cambia la escala si es preciso para visualizarlo mejor.
Expresaremos este hecho mediante la siguientes expresiones:
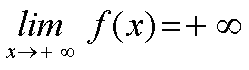 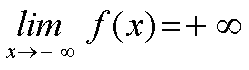
Y diremos que el límite de f(x) cuando x tiende a más infinito (o menos infinito, respectivamente) es más infinito. |
Los valores de la función f(x) decrecen indefinidamente cuando la variable independiente tiende a más infinito (o a menos infinito).
Desplaza la x hacia la derecha (o hacia la izquierda) en la imagen siguiente, tanto como quieras (cambia los valores de O.x para poder visualizarlo correctamente) y comprueba cómo f(x) se hace tan pequeña como se quiera (línea verde). Desplaza hacia abajo la gráfica y cambia la escala si es preciso para visualizarlo mejor.
¿Qué sucede cuando x=a?
Expresaremos este hecho mediante las siguientes expresiones:
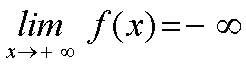 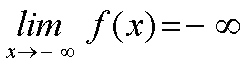
Y diremos que el límite de f(x) cuando x tiende a más infinito (o a menos infinito, respectivamente) es menos infinito. |
Los valores de la función f(x) ni se acercan a ningún valor concreto ni crecen ni decrecen indefinidamente cuando la variable independiente tiende a más infinito (o a menos infinito).
Desplaza la x hacia la derecha (o hacia la izquierda) en la imagen siguiente, tanto como quieras (cambia los valores de O.x para poder visualizarlo correctamente) y comprueba cómo los valores de f(x) (línea verde) van oscilando sin acercarse a ningún valor concreto. Además, aunque pueden hacerse tan grandes o tan pequeños como se quiera cuando x tiende a menos infinito siempre pueden encontrarse valores de f(x) negativos a la izquierda de cualquier valor positivo y valores de f(x) positivos a la izquierda de cualquier valor negativo.
| Expresaremos este hecho diciendo que la función f(x) no tiene límite ni en más infinito ni en menos infinito. |
OBSERVACIÓN
En los cuatro ejemplos anteriores el comportamiento de cada una de las funciones expuestas era similar tendiendo x a más infinito y a menos infinito. Sin embargo, en la realidad una función puede tener cualquiera de los cuatro comportamientos anteriores cuando x tiende a menos infinito y cualquiera de los otros cuando x tiende a más infinito.
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||