
En las páginas anteriores hemos visto de manera intuitiva el significado de límite de una función en un punto. Hemos analizado las distintas posibilidades que pueden presentarse y hemos empleado expresiones del tipo "acercarse a", "crecer indefinidamente", etc. Estas expresiones son un tanto vagas e imprecisas desde el punto de vista del rigor matemático.
Uno de los mayores logros de la Matemática de nuestro tiempo ha sido el fundamentar de manera precisa este concepto. Por ello en esta página vamos a intentar dar una definición rigurosa de límite en sus distintas variantes. Para ello partiremos de situaciones concretas sobre las que se irán planteando una serie de cuestiones y, a partir de las respuestas a esas cuestiones obtendremos las definiciones buscadas.
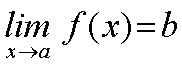
Como dijimos anteriormente, que este límite exista significa que cuando x "se acerca" al punto a, f(x) "se acerca" al punto b. La cuestión que se plantea inmediatamente es ¿qué entendemos por estar cerca? ¿a partir de qué momento se considera que dos números están cerca? Para cuantificar este acercamiento utilizaremos la siguiente notación:
|x-a| designa la distancia entre x y a.
Tradicionalmente suelen emplearse letras griegas minúsculas para designar distancias "pequeñas". En concreto suelen usarse las letras d (delta) para representar la distancia entre x y a y e (epsilon) para representar la distancia entre f(x) y b.
Hechas estas precisiones fíjate en la imagen siguiente y manípulala lo que consideres oportuno para responder a las cuestiones que la acompañan.
|f(x)-b| designa la distancia entre f(x) y b.
Del mismo modo suelen emplearse letras mayúsculas latinas intermedias (tales como, K, L, etc.) para representar números "muy grandes" en valor absoluto.
|
|
|
|
Si has conseguido hallar las respuestas a las preguntas anteriores te darás cuenta de que se puede obtener la siguiente conclusión: Si b es el límite de f(x) cuando x tiende al punto a, se cumple que sea cual sea el valor del número positivo e, es posible encontrar otro número positivo d, tal que si la distancia entre x y a es menor que d, entonces la distancia entre f(x) y b es menor que e.
Esta frase puede parecer enrevesada y difícil de comprender pero vamos a ver que en realidad significa lo mismo que la expresión "cuando x se acerca al punto a, f(x) se acerca al punto b". El problema radica en la expresión "acercarse" que evidentemente es arbitraria, pues una distancia puede representar cercanía en una determinada situación y la misma distancia puede representar lejanía en otra situación diferente. ¿Cómo solucionamos esta paradoja? Muy sencillo, se admite cualquier distancia como cercanía: decir "f(x) está cerca de b" equivale a decir "Sea e>0 cualquiera y |f(x)-b|<e".
Ahora bien, ¿cuando queremos que f(x) se acerque a b? Pues cuando x se acerque al punto a. Considerar que x y a estén cerca o lejos dependerá de qué hayamos considerado como cercanía en la distancia entre f(x) y b. El número que determina esa cercanía es el número arbitrario e, por lo que para cada valor que asignemos a este número deberá existir otro, d, que determine la cercanía entre x y a.
Por lo tanto la frase "si la distancia entre x y a es menor que d, entonces la distancia entre f(x) y b es menor que e". equivale a la frase "cuando x se acerca al punto a, f(x) se acerca al punto b".
Esto nos lleva a la siguiente
Definición
Diremos que b es el límite de la función f(x) cuando x tiende al punto a, cuando sea cual sea el valor del número positivo e, es posible encontrar otro número positivo d, tal que si la distancia entre x y a es menor que d, entonces la distancia entre f(x) y b es menor que e.
Simbólicamente esta definición se representa así:
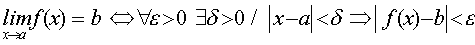
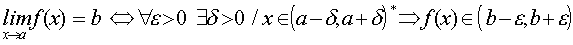
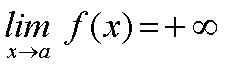
La idea intutitiva de esta situación nos decía que cuando x se acerca al punto a, f(x) va creciendo indefinidamente, es decir, podemos hacer que f(x) sea tan grande como se quiera sin más que hacer que x se acerque suficientemente al punto a.
De nuevo nos encontramos con conceptos algo ambiguos: "acercarse" y "hacerse grande". Al igual que en el caso anterior la cuestión principal es ¿a partir de qué valor consideramos que un número es grande? y ¿a qué distancia consideramos que dos números están cercanos?. Para responder a estas preguntas procederemos igual que en la situación anterior, es decir, partiremos de una situación concreta sobre la que se plantean una serie de cuestiones. Las respuestas a estas cuestiones nos permitirán definir con claridad los conceptos antes mencionados.
Hechas estas precisiones fíjate en la imagen siguiente y manípulala lo que consideres oportuno para responder a las cuestiones que la acompañan.
|
|
Si has conseguido hallar las respuestas a las preguntas anteriores te darás cuenta de que se puede obtener la siguiente conclusión: Si el límite de f(x) cuando x tiende al punto a es infinito, se cumple que sea cual sea el valor del número real K, es posible encontrar otro número positivo d, tal que si la distancia entre x y a es menor que d, entonces f(x) es mayor que K.
En otras palabras, estamos diciendo que cuando x se acerca al punto a, f(x) crece indefinidamente; o dicho de otra forma: si queremos que f(x) sea grande, basta con que x se acerque al punto a suficientemente.
Esto nos lleva a la siguiente
Definición
Diremos que el límite de la función f(x) cuando x tiende al punto a es más infinito, cuando sea cual sea el valor del número real K, es posible encontrar otro número positivo d, tal que si la distancia entre x y a es menor que d, entonces f(x) es mayor que K.
Simbólicamente esta definición se representa así:
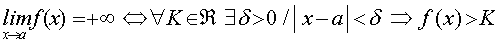
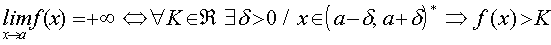
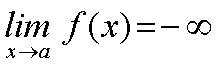
La idea intutitiva de esta situación nos decía que cuando x se acerca al punto a, f(x) va decreciendo indefinidamente, es decir, podemos hacer que f(x) sea tan pequeño como se quiera sin más que hacer que x se acerque suficientemente al punto a.
De nuevo nos encontramos con conceptos algo ambiguos: "acercarse" y "hacerse pequeño". Al igual que en el caso anterior la cuestión principal es ¿a partir de qué valor consideramos que un número es pequeño? y ¿a qué distancia consideramos que dos números están cercanos?. Para responder a estas preguntas procederemos igual que en la situación anterior, es decir, partiremos de una situación concreta sobre la que se plantean una serie de cuestiones. Las respuestas a estas cuestiones nos permitirán definir con claridad los conceptos antes mencionados.
Hechas estas precisiones fíjate en la imagen siguiente y manípulala lo que consideres oportuno para responder a las cuestiones que la acompañan.
|
|
Si has conseguido hallar las respuestas a las preguntas anteriores te darás cuenta de que se puede obtener la siguiente conclusión: Si el límite de f(x) cuando x tiende al punto a es menos infinito, se cumple que sea cual sea el valor del número real K, es posible encontrar otro número positivo d, tal que si la distancia entre x y a es menor que d, entonces f(x) es menor que K.
En otras palabras, estamos diciendo que cuando x se acerca al punto a, f(x) decrece indefinidamente; o dicho de otra forma: si queremos que f(x) sea pequeño, basta con que x se acerque al punto a suficientemente.
Esto nos lleva a la siguiente
Definición
Diremos que el límite de la función f(x) cuando x tiende al punto a es menos infinito, cuando sea cual sea el valor del número real K, es posible encontrar otro número positivo d, tal que si la distancia entre x y a es menor que d, entonces f(x) es menor que K.
Simbólicamente esta definición se representa así:
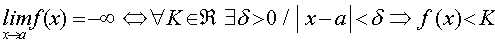
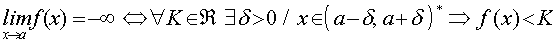
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||