6. Ecuaciones trigonométricas

Son aquellas en las que aparece alguna razón trigonométrica de la incognita. Para resolverlas es conveniente :

1º Expresar todas las razones que aparezcan en función de un mismo ángulo.

2º Expresar todas las razones en función de una sola razón trigonométrica.

Estos dos pasos se consiguen utilizando las fórmulas trigonométricas estudiadas anteriormente.

Las ecuaciones trigonométricas suelen tener múltiples soluciones que pueden expresarse en grados o en radianes.

Ejemplos de ecuaciones trigonométricas:

1ª sen(x)=1

2ª sen(2x)=2sen(x)

3ª cos²(x)-3sen(x)=3

Soluciones:

-La primera es muy sencilla, no hay que dar los pasos indicados, sólo recordar la circunferencia goniométrica y observar que 90º es el primer ángulo cuyo seno es 1. El seno no vuelve a valer uno hasta que el ángulo no valga 90º+360º=540º, tras otra vuelta volverá a valer uno y así sucesivamente. Luego hay muchas soluciones, todos los ángulos x de la forma x=90º+k.360º, donde k es cualquier número entero. Si queremos expresar la solución en radianes x=p/2+2.k.p radianes.

-La segunda necesita que apliquemos el primer paso. Como sen(2x)=2sen(x).cos(x), podemos escribir la ecuación en la forma 2sen(x).cos(x)=2sen(x). Ahora si dividimos por 2 nos queda sen(x).cos(x)=sen(x).Y si además dividimos por sen(x) queda cos(x)=1. Cuidado porque esta división supone que sen(x) es distinto de 0.

Las soluciones de cos(x)=1 son x=0º+k.360º o bien x=2.k.p radianes. Obtenidas razonando sobre la circunferencia goniométrica, como anteriormente.

Cuando sen(x)=0 no podemos dividir, esto ocurre para x=0º, 180º, 360º,...

es decir x=k.180º. Pero estos valores son soluciones de la ecuación puesto que cuando sen(x)=0 también sen(x).cos(x)=sen(x), ya que queda 0=0.

Ahora bien las soluciones de sen(x)=0 incluyen a las de cos(x)=1, por tanto las soluciones de la ecuación pedida son x=k.180º o bien x=k.p radianes.

- La tercera se convertirá en una ecuación con una sóla razón trigonométrica si tenemos en cuenta la fórmula fundamental de la trigonometría.

Pasaremos de cos²(x)-3sen(x)=3 a la ecuación 1-sen²(x)-3sen(x)=3, ordenando y agrupando queda sen²(x)+3sen(x)+2=0. Ya está en función de una sóla razón y de un sólo ángulo.

Cambimos ahora sen(x) por z y nos quedará z²+3z+2=0. esta ecuación tiene las soluciones z=-1 y z=-2, que nos proporcionan sen(x)=-1 y sen(x)=-2.

sen(x)=-1 tiene como soluciones x=270º+k.360º o bien x=3p/2+2.k.p radianes.

sen(x)=-2 no tiene solución alguna. Recurrimos continuamente a la circunferencia goniométrica.

Luego las soluciones de la tercera ecuación son: x=270º+k.360º o bien x=3p/2+2.k.p radianes.

El nippe Descartes nos permite utilizar un metodo distinto para obtener las soluciones:

Consiste en:

1- Igualar a 0 el segundo miembro de la ecuación, pasando todas las expresiones al primero.

2- Representar la función correspondiente al primer miembro de la ecuación. Esto se consigue escribiendola en la parte inferior de la escena y pulsando intro.

Las soluciones son las x de los puntos de contacto o de corte de la gráfica con el eje X.

Para saber esas coordenadas desplazamos con el ratón el punto marcado con x hasta el sitio de contacto o de corte. Suele haber muchas soluciones.

Para mejorar la precisión podemos aumentar la escala con lo que nos situaremos mejor sobre el punto buscado.

Los dos cuadros siguientes muestran la escena con distinta escala.

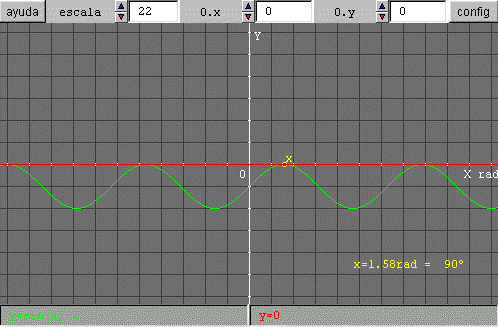
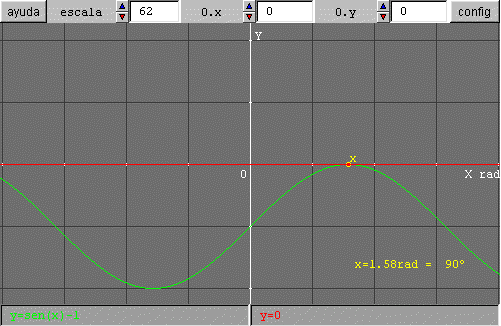
Ejercicio:

Prepara la escena para que puedas situarte sobre 4 soluciones distintas.

La siguiente escena está preparada para resolver la segunda ecuación.

Debes escribir en la parte inferior izquierda y=sen(2*x)-2*sen(x), en lugar de y=0

Si lo haces correctamente conseguirás:

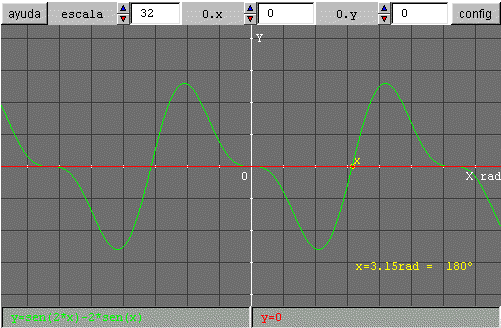
Como ves, x está situado sobre la solución 180º, también 0º es solución e infinitas más situadas a intervalos de 180º.

Recuerda que la variable independiente siempre debe ser x y no olvides los paréntesis y los signos de operación.

Para resolver la tercera ecuación debes escribir y=(cos(x))^2-3*sen(x)-3

El signo ^ se consigue pulsando la tecla Alt, y sin soltarla, 94 en el teclado numérico.

Pulsa inicio en la escena anterior para que quede preparada para recibir estos datos.

Un cuadro como el siguiente aparecerá si te lo propones.

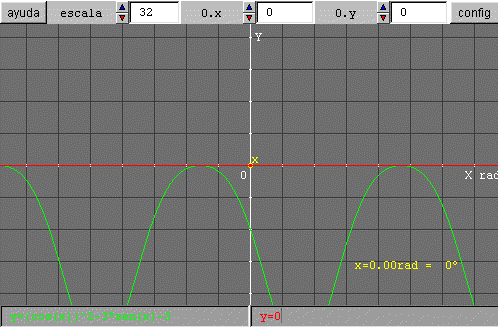
Cambiando la escala y arrastrando el punto x podrás determinar con bastante precisión las soluciones.

	Ministerio de Educación, Cultura y Deporte. Año 2000