
POLINOMIOS (1)
Operaciones con Polinomios:
Definición y ejemplos de polinomios
Un polinomio es una expresión algebraica que se obtiene al expresar cualquier suma de monomios no semejantes.
Si recordamos la suma de monomios, cuando estos no eran semejantes, no se podían sumar. En este caso lo que se obtiene es por tanto un polinomio.
Ejemplo 8.- Son polinomios las expresiones siguientes:
a) 4ax4y3 + x2y + 3ab2y3
b) 4x4 -2x3 + 3x2 - 2x + 5
En el primer caso el polinomio consta de la suma de tres monomios, cada uno de ellos es un término del polinomio, luego tiene tres términos., cada uno con varias letras, mientras que en el segundo caso el polinomio tiene 5 términos. Si un término sólo consta de un número se le llama término independiente (5 en el caso b y no existe en el caso a)
Cuando un polinomio consta de dos monomios se denomina binomio: x2y + 3ab2y3 ; 2x + 3 son dos binomios
Cuando consta de tres monomios se denomina trinomio: el caso a) anterior o -2x3 + 3x2 + 5 son dos trinomios.
Con más de tres términos (monomios) ya se denomina en general polinomio.
Respecto al grado de un polinomio, se dice que tiene por grado el mayor de los grados de los monomios que lo forman.
Así en el caso a) los grados de los monomios (suma de los exponentes de las letras) son 8, 3 y 6, luego el grado del polinomio es 8.
En el caso b) el grado es 4.
Los números que acompañan como factores a las letras (coeficientes de los monomios), se llaman también coeficientes del polinomio: 4 , -2 , 3 , -2 , y 5 respectivamente en el caso b).
" Lo más habitual que nos vamos a encontrar son polinomios del tipo del caso b), por tanto con una sola letra, que habitualmente será la x". En este caso a la letra se le suele llamar variable.
La siguiente escena sirve para comprobar estos conceptos en un polinomio con una sola letra.
La suma de polinomios se basa en la de monomios ya vista en este tema. Se podrán sumar los términos (monomios) que sean semejantes de los polinomios objeto de la suma.
"A partir de este momento trabajaremos ya sólo con polinomios con una sola letra (x) por considerar que son los más utilizados en la práctica "
Ejemplo 9.- Para calcular la suma de los polinomios:
(4x4 - 2x3 + 3x2 - 2x + 5 ) + ( 5x3 - x2 + 2x )
Basta sumar los términos de grados 3, 2 y 1 de ambos polinomios y dejar el resto de los términos del primero como está.
Podemos indicar la suma de la siguiente forma para verla mejor:
4x4 - 2x3 + 3x2 - 2x + 5
+--- - 5x3 --- x2 +2x
_____________________
4x4 + 3x3 + 2x2 + -----5
Por tanto: Para sumar dos o más polinomios se suman los términos semejantes de cada uno de ellos.
Si en lugar de sumar dos polinomios se tratara de restarlos, bastaría cambiar el signo a todos los términos del segundo y sumar los resultados.
Ejemplo 10.- Para calcular la diferencia o resta de los dos polinomios anteriores:
(4x4 - 2x3 + 3x2 - 2x + 5 ) - ( 5x3 - x2 + 2x )
Se calcula la suma: (4x4 - 2x3 + 3x2 - 2x + 5 ) + ( - 5x3 + x2 - 2x ) = 4x4 - 7x3 + 4x2 - 4x + 5
La escena siguiente presenta la suma y la resta de dos polinomios de grado máximo 3, siendo posible cambiar los coeficientes de cada uno de ellos. Téngase en cuenta que si un coeficiente es 0, el término correspondiente vale 0, luego no suma ni resta y viceversa, si "falta" un término podemos suponer que el coeficiente es 0.
Ejercicio 6.- Calcula en tu cuaderno de trabajo la suma y la resta
de los dos siguientes polinomios.
La suma del caso a) es la que se presenta en la escena siguiente.
Cambia después los valores de los coeficientes (se llaman c1 a
c4 para el primer polinomio y c5 a c8 para el segundo) de la
escena para realizar la resta del caso y la suma y resta del caso
b).
a) ( - x3 + 5x2 - x + 1 ) + ( 5x2 - x - 3 ) ; ( - x3 + 5x2 - x + 1 ) - ( 5x2 - x - 3 )
b) ( 6x2 - x + 4 ) + ( 5x3 - x - 1 ) ; ( 6x2 - x + 4 ) - ( 5x3 - x - 1 )
Para multiplicar dos polinomios se deben multiplicar todos los monomios de unos por todos los del otro y sumar los resultados. ("Atención especial al producto de potencias de la misma base")
Si uno de los dos polinomios es un monomio, la operación es simple como se puede ver en la escena siguiente, en la que se pueden variar los coeficientes.
En el caso en que ambos polinomios consten de varios términos, se puede indicar la multiplicación de forma semejante a como se hace con número de varias cifras, cuidando de situar debajo de cada monomio los que sean semejantes.
En la siguiente imagen se puede ver el producto de dos polinomios de varios términos.
Ejemplo 11.-
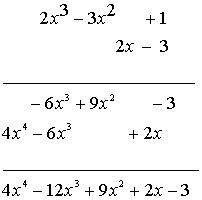
En la práctica no suele indicarse la multiplicación como en esta imagen, sino que suelen colocarse todos los términos seguidos y sumar después los que sean semejantes. Así:
Ejemplo 12.- ( - 2x3 + 3x2 - 2x + 5 ) · (x + 1) = (-2x4 +3x3 -2x2 + 5x - 2x3 + 3x2 - 2x + 5) = - 2x4 + x3+ x2 +3x + 5
Se denominan así a algunas operaciones con polinomios de especial interés ya que aparecerán frecuentemente en los cálculos.
Las más usuales son:
Cuadrado de un binomio: suma (a + b)2 o diferencia (a - b)2
Naturalmente realizar un cuadrado es multiplicar el binomio por sí mismo, luego:
(a + b)2 = (a + b ) · (a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2
" El cuadrado de una suma es igual al cuadrado del primero más dos veces el primero por el segundo más el cuadrado del segundo "
De modo similar: (a + b)2 = a2 - 2ab + b2 ( igual que antes pero cambiando el signo central).
"En cualquier caso se debe tener en cuenta que el primer término "a" también puede ser negativo y por tanto cambiar el signo central". "En general se puede considerar siempre como una suma y para cada término asignarle el signo que le preceda (ver ejemplo 13 - b)
Ejemplo 13.-
a) (2x + 3y)2 = (2x)2 + 2 · 2x · 3y + (3y)2 = 4x2 +12xy + 9y2
b) (- x + 3)2 = (-x)2 + 2 · (-x) · 3 + 32 = x2 - 6x + 9
Suma por diferencia: se refiere al producto de la suma de dos monomios por la diferencia de ellos mismos:
(a + b) · (a - b) = a2 - ab + ba + b2 = a2 - b2
Siempre recordamos que " suma por diferencia es igual a la diferencia de los cuadrados" .
Otras igualdades importantes pero menos utilizadas pueden son:
Cubo de una suma: (a + b)3 = a3 + 3a2b + 3ab2 +b3
Cuadrado de un trinomio: (a + b + c)2 = a2+ b2 +c2 + 2ab+ 2ac + 2bc
Ejercicio 7.- Calcula los siguientes productos notables:
a) (x + 2y)2
b) (2x2 - y)2
"El resultado del apartado a) puedes verlo en la siguiente escena. Cambia los coeficientes en la parte inferior de la escena y los exponentes de las letras en la parte superior para comprobar el b) y otros resultados que desees".
Ejercicio 8.- Calcula los siguientes productos notables:
a) (2a + 3b) (2a - 3b)
b) (-3a + b2) (-3a - b2)
"El resultado del apartado a) puedes verlo en la siguiente escena. Cambia los coeficientes en la parte inferior de la escena y los exponentes de las letras en la parte superior para comprobar el b) y otros resultados que desees".
La división de polinomios, en general se realiza de forma semejante a la de números de varias cifras, aunque las operaciones que realizamos rápidamente con los números, con los polinomios las vamos indicando. El proceso es el siguiente:
Con los polinomios dividendo y divisor ordenador de mayor a menor grado:
- Se divide el primer término del dividendo entre el primero
del divisor, dando lugar al primer término del cociente
- Se multiplica dicho término por el divisor y se coloca debajo
del dividendo con los signos contrarios, cuidando que debajo de
cada término se coloque otro semejante
- Se suman los polinomios colocados al efecto, obteniéndose un
polinomio de grado menor al inicial
- Se continua el proceso hasta que el resto ya no se pueda
dividir entre el divisor por ser de menor grado.
Normalmente se dividen polinomios con una sola variable (x) tanto en el dividendo como en el divisor. En la imagen siguiente se puede ver una división completa:
Ejemplo 14.-
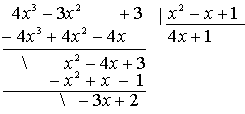
Como se ve se ha obtenido de cociente 4x + 1 y de resto - 3x + 2.
Ejercicio 9.- Realizar la división del polinomio 3x3 - 2x2 - 4x - 4 entre el binomio x - 2
(Se debe obtener de cociente 3x2 + 4x + 4 y de resto 4)
Precisamente el tipo de cocientes del ejercicio 9 es el más usual en la división de polinomios y a él dedicaremos el apartado siguiente.
Autor: Leoncio Santos Cuervo
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||