|
|
|

LÍMITE Y CONTINUIDAD DE FUNCIONES |
5.2.- Límite en un punto en el que la función no es contínua
Distinguimos dos casos:
5.2.1.- Funciones definidas de forma natural
Con las funciones que conoces hasta ahora, los únicos límites en puntos donde no son
contínuas son los de cocientes de funciones en donde se anula el
denominador.
Por ejemplo:
|
|
|
En las páginas siguientes estudiaremos con detalle los límites de cocientes de
polinomios. Para los demás casos es muy útil la calculadora.
En la siguiente escena vamos a hallar el límite, simulando el uso de la calculadora,
de la función ![]() , que no es contínua en x=0, pues f(0)=0/0.
, que no es contínua en x=0, pues f(0)=0/0.
Damos a x valores próximos a cero.
Para ello tenemos en la escena un punto P,
del cuál podemos introducir su abcisa x
Introduce en la escena, con las flechas, los valores de x cada vez más cerca de cero, y anota en tu cuaderno los valores correspondientes de la función:
|
Con el teclado y pulsando ENTER, introduce los valores de x, aún más cerca de cero:
x |
f(x) |
0.05 |
|
0.01 |
|
-0.01 |
Ya puedes deducir cuál es el ![]() , anótalo en tu cuaderno.
, anótalo en tu cuaderno.
Verás que si haces x=0 no aparace el valor de la función ni el punto P.
La función no está definida en x=0 pero existe ![]()
5.2.2.- Funciones construidas artificialmente empalmando dos o más trozos
En este caso para hallar el límite de la función en los puntos
donde se han empalmado los trozos, se halla el límite por la derecha y por la izquierda
en dichos puntos. Si ambos coinciden, ése será el límite, si no coinciden no existe el
límite.
Ejemplo: Hallar el ![]() de la función
de la función 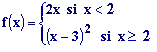
Damos a x valores por la izquierda de 2:
Introduce en la escena los valores de x, y anota en tu cuaderno los valores
correspondientes de la función
x |
f(x) |
1 |
|
1.2 |
|
1.4 |
|
1.6 |
|
1.8 |
Ahora ya puedes saber el límite de f(x) cuando
|
Ahora ya puedes saber el límite de f(x) cuando x ® 2+
Analíticamente es: ![]()
Como no coincide el límite por la izquierda y por la derecha de 2, no existe ![]()
6.- Cálculo
del límite de un cociente de polinomios
cuando x®a
Para hallar el ![]() (cociente de dos polinomios)
procederemos del siguiente modo:
(cociente de dos polinomios)
procederemos del siguiente modo:
¿Se anula el denominador en a? ¿Q(a)=0? |
NOÞ | Si Q(a)¹0 | ||
| SIÞ | ¿Se anula también el numerador en a? ¿P(a)=0? |
NOÞ | Si Q(a)=0 y P(a)¹0 | |
| lim f(x) = ±¥ x®a para decidir si es + o -, se estudia el signo a la izquierda y a la derecha de a |
||||
| SIÞ | Si Q(a)=0 y P(a)=0 | |||
y se vuelve al inicio del estudio |
EJERCICIO 13
Con las indicaciones dadas y la ayuda de esta escena, calcula los siguientes límites:
| a) b) c) En esta función se anula numerador y denominador para x=2, por tanto se puede dividir numerador y denominador entre (x-2). Al hacerlo se simplifica la fracción, quedando la misma función que en los apartados anteriores. |
EJERCICIO 14
Con las indicaciones dadas y la ayuda de esta
escena, calcula los siguientes límites:
| a) b) c) |
Autora: Ángela Núñez Castaín
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||