GEOMETRÍA ANALÍTICA

7.- Relación entre las pendientes m₁ y m₂ de dos rectas r₁ y r₂

rectas	r₁: y = m₁x + n₁
	r₂: y = m₂x + n₂
ángulo a
paralelas	a = 0º	m₁ = m₂
perpendiculares	a = 90º	1 + m₁.m₂ = 0
		m₁.m₂ = -1

En la siguiente escena tenemos dos rectas r₁: y = m₁x + n₁ r₂: y = 0.5x + 1
Los valores de m₁ y n₁ los podemos cambiar. En el inicio tenemos r₁: y = -0.2x + 4
Si cambias los valores de m₁ y n₁, verás como va cambiando el ángulo a entre las dos rectas.

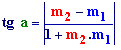EJERCICIO 21

1.- En el inicio de la escena m₁ = -0.2 y m₂ = 0.5
Aplica la fórmula dada, con la calculadora, para comprobar el ángulo a que nos da la escena.

2.- Introduce el valor de m₁ adecuado para que las rectas queden paralelas.
Compruébalo en la escena.

3.- Introduce el valor de m₁ adecuado para que las rectas queden perpendiculares.
Compruébalo en la escena.

4.- Hallar, en la escena, el ángulo que forman las rectas
r₁: x +y + 3 = 0 y r₂:x - 2y + 2 = 0 (pásalas primero a forma explícita)

5.- Escribe la ecuación explícita e implícita de la recta paralela a r₂ que pasa por el punto (0,-2). Compruébalo en la escena.

6.- Escribe la ecuación explícita e implícita de la recta perpendicular a r₂ que pasa por el origen.

Volver al índice

8.- Posición relativa de rectas dadas en forma general

Sistema con las rectas
Solución única	Se cortan en 1 punto
No tiene solución	Paralelas
Infinitas soluciones	Son la misma recta

En la siguiente escena tenemos dos rectas r: Ax + By + C = 0 r': x - 4y + 4 = 0
Los valores de A, B y C los podemos cambiar. En el inicio tenemos r: x - 3y + 12 = 0

EJERCICIO 22

1.- Comprueba que en el inicio es y que por tanto las rectas se cortan en un punto.

2.- Calcula en tu cuaderno las coordenadas del punto de intersección de r y r', resolviendo el sistema entre sus ecuaciones.

3.- Para comprobar el resultado tienes que desplazar los ejes con los botones de la parte superior de la escena, y pulsando con el ratón en el punto de intersección de las dos rectas verás sus coordenadas.

4.- Si das los valores A=2, B=-8 y C=16, esto es, r: 2x - 8y + 16 = 0 r': x - 4y + 4 = 0 se cumple que , por tanto las rectas serán paralelas.
Compruébalo en la escena.

5.- Si das los valores A=2, B=-8 y C=8, esto es,

r: 2x - 8y + 8 = 0 r': x - 4y + 4 = 0 se cumple que por tanto r y r' son la misma recta. Al comprobarlo en la escena da la sensación que desaparece una de las rectas, pero en realidad es que se superponen, lo notarás por el color, la azul tapa a la roja.

6.- Siendo siempre

r': x - 4y + 4 = 0 intenta averiguar, sin hacer cálculos, la posición entre r y r' en los siguientes casos: a) r: -3x + 12y + 5 = 0 b) r: -5x + 20y -20 = 0 c) r: 2x - 5y -1 = 0 En el caso de que se corten, calcula el punto de intersección. Compruébalo todo en la escena.

7.- Inventa tu valores de A, B y C, para que las rectas se corten, sean paralelas o coincidan. Luego compruébalo en la escena.

Volver al índice

Autora: Ángela Núñez Castaín


	Ministerio de Educación, Cultura y Deporte. Año 2000