GEOMETRÍA ANALÍTICA

6.- Ecuación explícita de la recta. Pendiente

Si en la ecuación implícita Ax + By + C = 0 es B¹0, podemos despejar la y, obteniendo una ecuación de la forma:

y = mx + n

Ecuación explícita de la recta

m es la pendiente de la recta
n es la ordenada en el origen

6.1.- SIGNIFICADO DE LA PENDIENTE DE UNA RECTA

La pendiente de una recta es el incremento de la ordenada (y), cuando la abcisa (x) se incrementa en una unidad.

Es fácil ver también, que la pendiente de una recta es la tangente trigonométrica del ángulo a que forma la recta con la parte positiva del eje X:

En esta escena puedes comprobar las dos cosas:

1.- Si cambias el valor de x₀, verás que en cualquier punto de una determinada recta, cuando la x se incrementa una unidad, y pasa de x₀ a x₀₊₁, la y se incrementa siempre lo mismo, m unidades.

Si cambias el valor de m, la inclinación de la recta varía.

La ordenada en el origen, n, es el valor de y cuando x=0, o sea que la recta corta al eje Y en el punto (0,n). Puedes comprobarlo variando n en la escena.

2.- Como puede verse, se nos forma un triángulo rectángulo, donde el cateto opuesto al ángulo a, es m, y el contiguo vale 1. Por esta razón, la pendiente también controla la dirección de la recta.

3.- En esta escena puedes cambiar el valor de la pendiente m, de la recta, y se irán dibujando diferentes rectas con diferentes pendientes.

Así verás más claro el significado de la pendiente.

Observa la diferencia entre las rectas de pendiente positiva, las de pendiente negativa, y las de pendiente cero.

4.- Pulsa el botón limpiar, y cambia el valor de la ordenada en el origen, n. Podrás observar qué diferencia hay entre rectas de la misma pendiente con diferentes valores de n.

6.2.- OBTENCIÓN DE LA PENDIENTE DE UNA RECTA A PARTIR DE DOS DE SUS PUNTOS

La pendiente de la recta que pasa por P₁(x₁,y₁) y P₂(x₂,y₂) es:

En esta escena puedes cambiar los puntos P₁ y P₂, y comprobar que la pendiente, m, sigue siendo la misma para una recta determinada.

También puedes cambiar el valor de m, obteniéndose rectas con distintas pendientes.

EJERCICIO 17

1.- Da al botón inicio de la escena.

2.- Copia en tu cuaderno las coordenadas de los puntos P₁(x₁,y₁) y P₂(x₂,y₂)

3.- Aplica la fórmula que hemos dado para hallar la pendiente, m.

4.- Comprueba el valor de m que te ha dado, en la escena.

5.- Calcula la pendiente de la recta que pasa por los puntos P₁(1,2) y P₂(4,5). Introduce el valor obtenido en la escena, y a continuación los valores de x₁=1 y x₂=4, de esta forma comprobarás tus cálculos.

6.- Calcula la pendiente de la recta que pasa por los puntos P₁(-2,5) y P₂(1,-1). Introduce el valor obtenido en la escena, y a continuación los valores de x₁=-2 y x₂=1, de esta forma comprobarás tus cálculos.

6.3.- FORMA PUNTO-PENDIENTE DE LA ECUACIÓN DE UNA RECTA

Si de una recta conocemos un punto P(x₀,y₀) y su pendiente m, su ecuación es:

y = y₀ + m(x - x₀)

Es evidente que pasa por (x₀,y₀) y que su pendiente es m

En la siguiente escena está representada y calculada la ecuación de la recta que pasa por el punto P(-2,1) y tiene de pendiente m = -3/4 = -0.75

Puedes variar las coordenadas del punto P y la pendiente m, en los botones inferiores, para ver como varía la gráfica de la recta y su ecuación. Ésta aparece también en forma implícita.

EJERCICIO 18

1.- Sustituye en la ecuación PUNTO-PENDIENTE, las coordenadas de P y el valor de m, y calcula la ecuación implícita de la recta.

2.- Escribe en tu cuaderno la ecuación PUNTO-PENDIENTE de la recta que pasa por el punto P(4,3) y tiene de pendiente m=1.8

3.- Calcula su ecuación implícita.

4.- Compruébalo en la escena.

EJERCICIO 19

Hallemos la ecuación de una recta, conociendo dos puntos A(-3,1) y B(7,6)

1.- Primero tienes que calcular su pendiente, que ya sabes hacer conociendo dos puntos.

2.- Aplica la ecuación PUNTO-PENDIENTE tomando cualquiera de los dos puntos conocidos, por ejemplo A (el resultado final será el mismo si tomas B).

3.- Halla la ecuación implícita.

4.- Comprueba que tomando el punto B en vez del A, la ecuación implícita es la misma.

5.- Calcula la ecuación de la recta que pasa por los puntos (-4,5) y (4,2)

6.- Calcula la ecuación de la recta que pasa por los puntos (-2,5) y (7,5). ¿Cuál es la pendiente en este caso? Sin hacer cálculos, ¿cuál sería la ecuación y la gráfica si los puntos son (1,-2) y (5,-2)?

7.- Ahora los puntos son (3,8) y (3,-2). En este caso siempre vale x=3, luego la ecuación de la recta es x=3. Es una recta paralela al eje Y. No tiene pendiente. No se puede poner de forma explícita porque hay una división por cero. Pruébalo en la escena. (¡Atención! No es correcto decir que su pendiente es infinita)

EJERCICIO 20

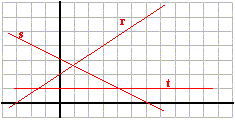
1.- Escribe las ecuaciones de las rectas representadas en esta figura:

2.- Para comprobar los resultados, utiliza esta escena. En ella aparece dibujada la recta y = 0, o sea la que tiene pendiente m=0 y ordenada en el origen, n=0.

3.- Cuando le des a m y a n los valores obtenidos en la primera recta, se dibujará ésta. Pero permanecerá la recta y=0. Si quieres borrarla, pulsa el botón LIMPIAR.
Puedes dibujar las tres rectas pedidas, sin que se borre una cuando introduzcas otra.
Si quieres borrarlas todas, pulsa el botón INICIO.
Cuando tengas las tres dibujadas mira la figura de arriba y comprueba si todo es correcto.

Volver al índice

Autora: Ángela Núñez Castaín


	Ministerio de Educación, Cultura y Deporte. Año 2000