
GEOMETRÍA ANALÍTICA |
| Distancia entre dos puntos P(x1,y1), Q(x2,y2) es el módulo del vector PQ | 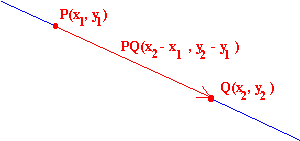 |
| dist(P,Q) = |PQ| = |
Vamos a hallar la distancia entre los puntos
P(3,-1) y Q(-1,2)
dist[(3,-1),(-1,2)]= ![]()
| Ahora puedes mover con el ratón
los puntos P y Q, o cambiar sus coordenadas en los botones inferiores,
para ir viendo la distancia PQ, para los distintos puntos.
EJERCICIO 12 1.- Calcula en tu cuaderno las coordenadas del vector PQ siendo P(3,-5) y Q(1,4) 2.-Calcula ahora la distancia PQ 3.- Comprueba el resultado en esta escena. 4.- ¿Cuáles son las coordenadas del vector PQ si P(1,4) y Q(3,-5)¿Cuál es ahora la distancia entre P(1,4) y Q(3,-5)? |
| La distancia del punto P(a,b) a la recta r:Ax + By + C = 0 es: | dist(P,r)
= |
1.- En la escena anterior, está calculada
la distancia del punto P(-5,8)
a la recta
r: 2x -6y + 7 = 0,
calcúlala tú en tu cuaderno aplicando la fórmula con
tu calculadora, y comprueba el resultado.
2.- Calcula la distancia de P(2,-1) a r: x - 3y + 5 = 0, y compruébalo en la escena anterior.
3.- Calcula la distancia de P(7,0)
a r: ![]() (primero tendrás que pasar r a forma implícita).
(primero tendrás que pasar r a forma implícita).
Comprueba el resultado
en la escena anterior.
4.- Si calculas la distancia de P(3,3) a r: y = 2x - 3 (primero tendrás que pasar r a forma implícita), verás que resulta igual a cero. ¿Cuál es el motivo para que esto ocurra? Míralo en la escena.
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||