Conocemos el vértice de las parábolas y=K*(x-m)^2 +n
Un poco de calculo:
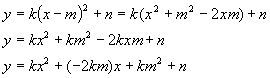
Habitualmente nosotros conocemos las parábolas de la forma y=ax^2+bx+c.
Comparamos la forma habitual con la que hemos obtenido en los cálculos de arriba y tenemos:
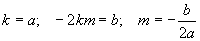

Mi parábola es distinta..........
Está claro si la gráfica es una parábola y tiene una ecuación de la forma y=K*(x-m)^2+n su vértice es V(m, n). Donde m y n pueden ser cualquier número y K cualquier número distinto de cero.
¿Mi parábola tiene una ecuación distinta? ¿Qué hago?
Vamos a buscar la relación entre y=4x-x^2 y una parábola de la forma y=K*(x-m)^2+n
Conocemos el vértice de las parábolas y=K*(x-m)^2 +n
Un poco de calculo:
Habitualmente nosotros conocemos las parábolas de la forma y=ax^2+bx+c.
Comparamos la forma habitual con la que hemos obtenido en los cálculos de arriba y tenemos:
Ya conocemos el valor de x donde está el vértice , para calcular el valor de y sustituimos en la ecuación de la parábola.
En mi problema la solución es:
Comprueba en la gráfica que las dos parábolas son iguales.(en la ecuación azul sustituye a,b,c por su valor y con las flechas pon los valores correspondientes de k, m y n).
Luego la solución es ancho=?, alto=?, área máxima=?. Es decir tengo que cortar cuatro listones.........(completa tu la frase)
Si en lugar de tener un listón de 8 lo tienes de "4", "6", "10"¿ Cuál es la solución?
Escribe la ecuación de tres parábolas, calcula su vértice y comprueba en la gráfica anterior que lo has hecho perfectamente.
- .
- Explica en tu cuaderno lo anterior y representa las gráficas que creas necesarias para recordar todo esto.
Enunciado tercer paso más problemas
Autora: Mª Teresa García Fernández