
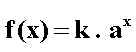
En el estudio de la función exponencial hay que tener en cuenta que la base a es > 0
6.-Vas a estudiar una función exponencial que te servirá como patrón de todas las funciones exponenciales de base > 1. Es f(x) = 2^x (dos elevado a x). Anota en tu cuaderno las carcterísticas más interesantes de la misma: Dominio, recorrido.
¿Quién es la imagen de 1?.Es decir, pasa por el punto (1 , 2) . ¿Y por el (0, )?. ¿Cuánto valdrá f(-1000)? ¿y f(500)?. ¿Se trata de una función creciente o decreciente.? ¿Tiene alguna asíntota?
Representa la gráfica de f(x) = 3^x , f(x) = 1.75^x , f(x) = 4^x. Anota en tu cuaderno, con cada una, las características que hallaste con la función patrón. Cuando hayas terminado observa las semejanzas y las diferencias entre ellas.
¿Quién crece más deprisa? ¿Hay un punto por el que pasan todas?. Si te dan una gráfica y no sabes cuál es el valor de a, ¿cómo podrías encontrarlo?
7.-Ahora estudiaremos una función exponencial patrón para cuando la base a toma un valor entre 0 y 1. Representa la gráfica de la función f(x)=0.5^x ( 1/2 elevado a x). Trata de responder a las mismas preguntas del apartado anterior.
Observa que en este caso te sale una gráfica decreciente, que cuando x se hace muy grande f(x) se parece a 0, y cuando es negativa muy grande tiene una imagen positiva y cada vez mayor. Sin embargo pasa por (0 , 1) y tiene el eje OX como asíntota, igual que todas las demás exponenciales.
Representa la gráfica de las funciones f(x) = 0.25^x , f(x) = 0.75^x. Anota las semejanzas y diferencias con la función patrón. ¿Cuál de las tres decrece más rápido?
¿Qué le ocurre a la gráfica de f(x) = 1^x? ¿Tienes una explicación?.
Resolución de problemas con funciones exponenciales
8.-En el contrato de alquiler de un apartamento figura que el precio subirá un 5% anual. Si se pagaban 25000 ptas. mensuales.¿cuánto pagaremos al mes dentro de 5 años?. Escribe la función que da el precio de alquilersegún los años transcurridos.¿Cuántos años tienen que pasar para pagar el doble?
Vamos a resolverlo despacito:
Si el alquiler de un año fuese 1 peseta al segundo año tendríamos que pagar 1+0.05=1.05
Si fuera de C pesetas tendríamos que pagar el segundo año C+ C*0.05 = C*(1+0.05) = C*1.05
Al tercer año pagaríamos (C*1.05)*1.05 = C* 1.05^2.
Así que, por este razonamiento, el quinto año pagaríamos C*1.05^4. Es decir 12*25000*1.05^4 = 300000*1.05^4.
Ahora vamos a la escena y damos a = 1.05 y llevamos P con el ratón hasta que Px valga 4. Anotamos que Py vale 1.22. Es decir 1.05^4 = 1.22. Ese año pagaremos cada mes 1.22*300000/12 = 30500 ptas.
La funcián que nos da el alquiler será 1/12 * 300000* 1.05^x = 25000*1.05^x
Ahora nos preguntan cuánto tiene que valer x para que 25000*1.05^x = 50000, o lo que es lo mismo, cuánto tiene que valer x para que 1.05^x =2.
Vamos a la escena y movemos la escala y el punto P hasta que, si a=1.05 , Py valga 2. Vemos que Px vale en ese caso 14.21. luego tendrán que pasar algo más de 14 años.
9.-En el contrato de trabajo de un empleado figura que su sueldo subirá un 8% anual. Si empieza ganando 1 800 000 ptas anuales, ¿cuánto ganará al cabo de 10 años? ¿Cuánto tiempo tardará el sueldo en duplicarse?
10.-Se sabe que la concentración en sangre de cierto tipo de anestesia viene dada por la fórmula y=90*0.95^t donde 90 es la dosis inicial en mg y t los minutos desde que se administró.
a) ¿Qué cantidad de anestesia tiene el paciente al cabo de 10 minutos? ¿Y de una hora?
b) Se va a realizar una operación que tardará media hora y, para que se desarrolle bien es necesario que la cantidad de anestesia en el paciente no sea inferior a 27 mg. ¿Al cabo de cuántos minutos hay que inyectarle de nuevo? (0.95^x = 27/90).
Autora: Clara Aranzana Angulo