
Función Proporcionalidad Inversa
Funciones Exponencial y Logarítmica
Función Proporcionalidad Inversa
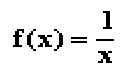
Un rectángulo tiene un metro cuadrado de superficie, si uno de los lados mide x metros, ¿cuánto mide el otro lado? . La respuesta viene dada por 1/x. Así pues la función f(x) = 1/x llamada de proporcionalidad inversa da respuesta al problema
Actividades:
1.- Utiliza los controles de escala, x , Ox y Oy si es necesario para escribir en tu cuaderno los valores de
f(1) , f(3), f(4.6) f(-3) f(-0.2) f(-7) f(130) f(-20) y f(0.01).( En caso de que se te descomponga la gráfica demasiado puedes volver al comienzo pulsando el botón Inicio)
Escribe en cada caso las coordenadas del punto P.
¿Qué valor le daríamos a f(0)? ¿Por qué?. Escribe en tu cuaderno el dominio de la función f(x)=1/x
2.-Los ejes coordenados parecen "sujetar" la curva en puntos del infinito. Cuando una recta está en estas circunstancias respeto de una curva se la llama asíntota. Escribe en tu cuaderno las ecuaciones de esas dos rectas
Otras formas de la función proporcionalidad inversa.
La función f(x) = k / x
4.-Manteniendo constantes los valores de k=1 y b=0 escribe en tu cuaderno las características de la función f(x) = 1/ (x-2) (Esta es la forma en que aparece escrita la función en la parte inferior de la escena.Fíjate bien pues alguna vez vas a tener que utilizarlo).¿Quiénes son las asíntotas?
Haz lo mismo con las funciones f(x) = 1/(x+1) y f(x) = -1/(x+1)
¿Puedes deducir que las asíntotas de la función f(x)=k/(x-a) son x=a e y=0? ¿En qué influye el signo de k? ¿Y su valor absoluto?
Estudio de la función
![]()
5.-Manteniendo los valores de k =1 y b = 0, observa la gráfica de la función f(x) = 1/ (x-1). Escribe en tu cuaderno cuál es su dominio. Escribe también las ecaciones de sus asíntotas. Haz lo mismo para las funciones f(x) = 1/ (x-2) , f(x) = 1/ (x+1) y f(x) = -2 / (x-1).
¿Puedes concluir que las asíntotas de f(x) = k / (x-a) son x = a e y = 0? .¿Qué papel hace el signo de k?. ¿Qué papel hace el valor absoluto de k?.
6.-Haz lo mismo tomando como valores k=1, a = 0 y b=1.5. Observa la gráfica obtenida y escribe en tu cuaderno el dominio y las asíntotas de la función f(x) = 1/x + 1.5. Representa las funciones f(x)= 1/x - 1 , f(x)= 1/x +2 , f(x)= 2/x -3 , f(x)= -1/x +1. Escribe en tu cuaderno los valores del dominio y las asíntotas.
Seguro que has llegado a ver que el dominio de las funciones f(x) = k/x + b es R-{0} y sus asíntotas son x = 0 e y = b
7.- Representa las funciones f(x) = 2/ (x+3) -1 , f(x) = -1.25 / (x+1.5) +2 y f(x) = 3/(x-2)+1. Escribe las carcaterísticas más relevantes de cada una.
Concluye cuáles son el dominio, las asíntotas y el papel de k en la función f(x) = k/(x-a)+b.
Resolución de problemas utilizando la escena
8.-El coste por unidad de fabricación de unas pegatinas disminuye según el número de unidades fabricadas y viene dado por la función y = 50 + 100 / x. . Utiliza la escena para dibujar la gráfica.(Tendrás que cambiar la escala y mover los ejes para que sólo se vea la gráfica que es significativa para el problema)
¿Tiene sentido en el problema que esten todos los puntos unidos?. Calcula cuánto cuestan 20 pegatinas, 350 y 1500. Escribe el resultado en tu cuaderno (Para hacerlo puedes señalar con el ratón un punto de la gráfica y al pulsar el botón izquierdo salen sus coordenadas en la pantalla)
¿Cuál será el coste cuando el número de pegatinas es muy grande?
Reconocer una función proporcionalidad inversa dada su gráfica
9.-En esta actividad te sale en escena una gráfica en rojo cuya fórmula tienes que adivinar. Para ello basta con que sustituyas los valores de k, a, y b de la parte inferior de la escena por los adecuados y pulses la tecla Intro. Si has acertado, la gráfica en verde se colocará en el lugar donde estaba la gráfica roja. Si no es así, en el lugar de la gráfica roja aparecerá un rastro rosa. En este último caso, antes de probar de nuevo, haz click sobre el botón limpiar.
Intenta acertar 5 veces seguidas
Autora: Clara Aranzana Angulo