
Un
número complejo es una expresión de la forma z=a+bi.
A 'b' se le llama parte imaginaria y 'a' recibe el nombre
de parte real. La letra i
se llama unidad imaginaria y verifica que
i2=-1. También
puede definirse como el par ordenado (a,b).
La representación de un número complejo es el vector que une el origen de coordenadas con el punto (a,b), llamado afijo del número complejo.
1.- Dibuja, mediante las flechitas o poniendo directamente los valores de a y b mediante el teclado, los números complejos 2+5i, 3i, 8, -2-i, 3+3i, 3-3i
El
opuesto de un número complejo z=a+bi es
el número complejo -z=-a-bi. El
conjugado de z se define como
![]() =a-bi
=a-bi
2.-
Utiliza las flechas, el teclado o el ratón sobre el extremo del vector que
representa a z y observa la representación de z
, -z
y
![]() .
.
3.- ¿Qué número complejo es el que
tiene ?
en el afijo? ¿Cómo se puede poner en función de –z? ¿Y en función de
![]() ?
?
La
suma de dos números complejos es otro número complejo que tiene como parte
real la suma de las partes reales y como parte imaginaria la suma de las partes
imaginarias. Gráficamente es la diagonal del paralelogramo que determinan los
dos números complejos y que parte del origen.
Si
observas la representación del número complejo z1-z2, te darás cuenta de que
si lo representases partiendo de z2, obtendrías la otra diagonal del
paralelogramo.
La diferencia z1-z2 se obtiene sumándole a z1 el opuesto de z2.
4.- Para sumar o restar dos números
complejos puedes escribir las componentes (z1.x, z1.y, z2.x, z2.y), utilizar las
flechitas o ratón (moviendo los extremos de los números complejos z1 y z2).
Representa los números complejos 3+i, 3-i, -3+2i, -3-2i, 6, -5i.
Si tenemos dos números
complejos a+bi y c+di, el producto y el cociente se definen de la siguiente
forma
![]()
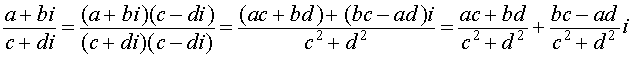
5.-Considera los números complejos z1=3+i y z2=3-i y calcula el producto y el cociente. Haz lo mismo con z1= -3+2i y z2=3i.
Autor:
José Antonio Jódar Gil
Sigue