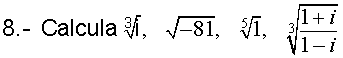Números complejos (II)
V.
Números complejos en forma polar.
Dado
un número complejo a+bi, el vector que lo representa forma un ángulo ang
con el semieje positivo del eje de abscisas que se llama argumento. Cualquier
número complejo queda determinado por el argumento y por el módulo
(distancia del origen al afijo) y se representa por rang:
6.-
El argumento es el arco-tangentede
b/a (¡ten cuidado con los cuadrantes!). Además: a=r*cos(ang)
y b=r*sen(ang). Compruébalo con los números complejos: 190º
, 3, 2pi/4, -1/2+3i, -8i, 1+i y-4.
7.-
Para multiplicar números complejos en forma polar basta con sumar
los argumentos y multiplicar los módulos. Para dividir se restan
los argumentos y se dividen los módulos. Compruébalo usando
este apartado y el anterior (IV).
VI. Radicación de números complejos.
Una
de las diferencias que más llaman la atención de los números
complejos es que cualquier número complejo tiene dos raíces
cuadradas (mientras que entre los números reales sólo lo
verifican los positivos). Pero hay más, un número complejo
tiene tres raíces cúbicas, que son los vértices de
un triángulo equilátero), cuatro raíces cuartas (que
son los vértices de un cuadrado), etc.
La
fórmula que nos permite calcular las n raíces n-ésimas
de ranges:
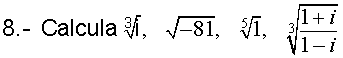
9.-
Resuelve las ecuaciones: x3-8=0, x4+1=0, x4-81=0.
Autor:
José Antonio Jódar Gil
Volver