En los circuitos digitales sólo hay 2 voltajes. Esto significa que al utilizar 2 estados lógicos se puede asociar cada uno con un nivel de tensión, así se puede codificar cualquier número, letra del alfabeto u otra información. Estos 2 estados de tensión reciben diferentes nombres, los más utilizados son estado lógico 0 y estado lógico 1, o bien falso y verdadero, respectivamente.
Al utilizarse sólo 2 estados lógicos (0 y 1) se dice que la lógica digital es binaria, ya que el código binario se basa en la utilización de dos únicas cifras, 0 y 1.
Una de las principales ventajas de este sistema es la sencillez de sus reglas aritméticas, que hacen de él un sistema apropiado para el uso de computadores y dispositivos digitales.
El sistema binario está en base 2, mientras que el sistema decimal (el más utilizado en el mundo) está representado en base 10.
A continuación se muestran las equivalencias entre los primeros números decimales y los binarios correspondientes.
DECIMAL |
BINARIO |
0 |
0 |
1 |
1 |
2 |
10 |
3 |
11 |
4 |
100 |
5 |
101 |
6 |
110 |
7 |
111 |
8 |
1000 |
9 |
1001 |
10 |
1010 |
11 |
1011 |
12 |
1100 |
13 |
1101 |
14 |
1110 |
15 |
1111 |
Existen 2 maneras diferentes de convertir un número decimal en un número binario.
Método 1: Se establece una tabla de equivalencias de las potencias de 2 con respecto a los números decimales. Como en el resto de códigos, la posición de cada cifra está ponderada, de la misma forma que en el código decimal la posición de las unidades "vale" 1, las decenas 10 y asi sucesivamente, la primera posición por la derecha, en los números binarios, "pesa" 1, la 2ª 2, la 3ª 4, la cuarta 8, etc.
Equivalencia decimal |
64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Potencias de 2 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
Ejemplo:
Para transformar un número decimal como el 54 a código binario, se deben coger las potencias cuya suma den el número elegido, las potencias a utilizar son: 25 + 24 + 22 + 21 = 32 +16+ 4 +2 = 54. Con lo cual el número 54 se representará en formato binario del siguiente modo: 110110.
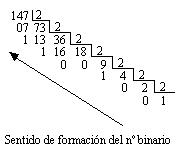
Método 2: Se realiza una serie de divisiones sucesivas del número decimal a convertir por el número 2 que es la base binaria. El resto de cada división realizada se guarda, ya que formará parte del número binario. Los restos de cada división se cogerán de manera ascendente como se muestra en el siguiente ejemplo.
Ejemplo:
El número 147 se convierte en un número binario de la siguiente manera, utilizando la división continuada.

Con lo cual el número 147 se representará en formato binario del siguiente modo: 10010011.
Las reglas son similares a las del sistema numérico decimal, aunque son mucho más simples al contar el sistema binario con tan solo 2 cifras (0 y 1). Las reglas fundamentales se muestran a continuación:
A continuación se muestra una serie de ejemplos de los anteriores operadores aritméticos.

Convendría tener en cuenta unas operaciones denominadas complementos que se utilizan principalmente para expresar números negativos, así como para realizar operaciones de restas mediante sumas.
Se denomina Complemento de una cifra a la diferencia entre la base y tal cifra Por ejemplo en el sistema octal, base 8, el complemeto del 3 sería el 8-3= 5. En el sistema binario se utilizan mucho estos 2 complementos:
Complemento a 1: Se obtiene escribiendo el opuesto al bit correspondiente, es decir, si es un 1 se pone un 0 y viceversa.
Ejemplo:
| Número: | 10010111 |
| Complemento a 1: | 01101000 |
Complemento a 2: Este complemento se puede hallar de 2 maneras distintas.
La 1ª forma consistiría en hallar primero el complemento a 1, y una vez hallado éste le sumariamos 1.
Ejemplo:
| 1 1 0 0 1 0 1 | Número del cual obtener el complemento a 2 | |
| 0 0 1 1 0 1 0 | Complemento a 1 | |
| +1 | Se suma 1 | |
| __________ | ||
| 0 0 1 1 0 1 1 | Complemento a 2 del número |
La 2ª forma consistiría en hallar la resta del número a complementar con respecto al número que empiece por 1 y vaya seguido de tantos ceros como bits tenga el número a complementar.
Ejemplo:
| 1 0 0 0 0 0 0 0 | ||
| -1 1 0 0 1 0 1 |
Número del cual obtener el complemento a 2 | |
| ____________ | ||
0 0 1 1 0 1 1 |
Complemento a 2 del número |
Complemento de 9 y de 10: El complemento a 9 de un número se halla por sustracción a 9 de cada dígito decimal.
Ejemplo:
9 9 9 |
Número con tantos "9" como cifras tiene el número a complementar | |
|
-5 0 1 |
Número a complementar | |
______ |
||
4 9 8 |
Complemento a 9 del número |
El complemento a 10 de un número es igual al complemento a 9 añadiéndole después 1. En el ejemplo, el complemento a 10 del número 501 será el número 499.
Aunque los circuitos electrónicos digitales y las computadoras utilizan el sistema binario, el trabajar con este sistema de numeración resulta laborioso, lo que facilita las equivocaciones cuando se trabaja con números binarios demasiado largos.
El sistema Hexadecimal está en base 16, sus números están representados por los 10 primeros dígitos de la numeración decimal, y el intervalo que va del número 10 al 15 están representados por las letras del alfabeto de la A a la F.
Actualmente el sistema hexadecimal es uno de los más utilizados en el procesamiento de datos, debido principalmente a 2 ventajas:
La primera ventaja es la simplificación en la escritura de los números decimales, cada 4 cifras binarias se representan por una hexadecimal.
La segunda es que cada cifra hexadecimal se pueden expresar mediante 4 cifras binarias, con lo que se facilita la trasposición entre estos 2 sistemas. Para convertir un número binario en hexadecimal se realiza el mismo proceso, pero a la inversa.
DECIMAL |
HEXADECIMAL |
BINARIO |
0 |
0 |
0000 |
1 |
1 |
0001 |
2 |
2 |
0010 |
3 |
3 |
0011 |
4 |
4 |
0100 |
5 |
5 |
0101 |
6 |
6 |
0110 |
7 |
7 |
0111 |
8 |
8 |
1000 |
9 |
9 |
1001 |
10 |
A |
1010 |
11 |
B |
1011 |
12 |
C |
1100 |
13 |
D |
1101 |
14 |
E |
1110 |
15 |
F |
1111 |
Ejemplo:
Número Hexadecimal: B7E16)
B: 1011 (11)
7: 0111 (7)
E: 1110 (14)
Número Binario: 1011 0111 1110
Para pasar el número hexadecimal al sistema decimal, se han de multiplicar los dígitos hexadecimales por las distintas potencias de base 16 que representan cada dígito del sistema de numeración hexadecimal.
Ejemplo:
B7E16) = 11•162 + 7•161 + 14•160 = 2816 + 112 + 14 = 2942 10)
A la inversa, para convertir el número decimal en hexadecimal, éste se irá dividiendo por el número 16 sucesivamente hasta que ya no se puedan realizar más divisiones con el mismo número. El número hexadecimal resultante estará formado por el último cociente seguido de todos los restos sucesivos obtenidos desde el último hasta el primero.
Ejemplo:
Nº Hexadecimal: 15E16)
Otra posibilidad en la conversión de números decimales y hexadecimales es utilizar los binarios como intermediarios, es decir, en cualquiera de los sentidos, se obtendría en primer lugar el número binario y después éste pasaría al código definitivo.
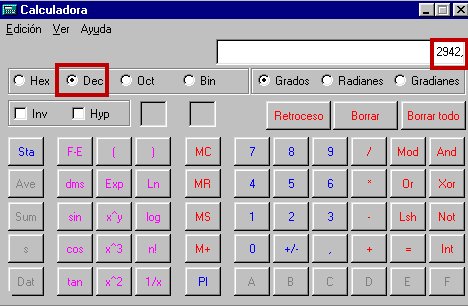
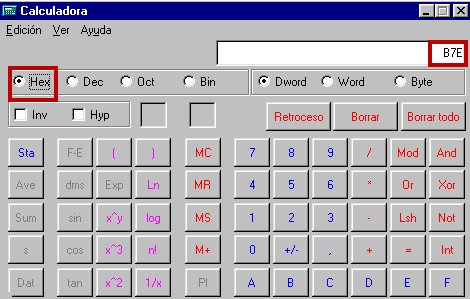
Por último, otra posibilidad de cálculo la ofrecen las calculadoras de sobremesa o las que suelen venir con algunos sistemas operativos. En ese caso basta teclear la cantidad estando seleccionado un sistema: binario, octal, hexadecimal o decimal, y después conmutar al sistema de destino deseado y el número aparecerá automáticamente:
El álgebra de Boole fue creada por George Boole a principios del siglo XIX para poder explicar las leyes fundamentales de aquellas operaciones de la mente humana por la que se rigen los razonamientos.
La numeración binaria y el álgebra de Boole constituyen la base matemática para el diseño y la construcción de dispositivos digitales.
Se entiende por Función Lógica toda aquella variable binaria cuyo valor depende de una expresión formada por otras variables relacionadas mediante los signos “+” y “x”. El comportamiento de las funciones lógicas se puede conocer a través de las tablas de verdad, dependiendo de los niveles que se apliquen a las entradas.
El álgebra de Boole se entiende mejor al describir las funciones básicas de este sistema de razonamiento. Las funciones básicas son las siguientes:
| Función | Dibujo esquemático |
| S = a |
a |
S |
|---|---|
0 |
0 |
1 |
1 |
| Función | Dibujo esquemático |
| S = - a |
a |
S |
|---|---|
0 |
1 |
1 |
0 |
| Función | Dibujo esquemático |
| S = a + b | 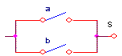 |
| a | b | S |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
| Función | Dibujo esquemático |
| S = a · b |
| a | b | S |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Las operaciones lógicas de adicción y multiplicación tienen una serie de propiedades entre las que destacan las siguientes:
Conmutación:
a + b = b + a
a · b = b · a
Identidad:
0 + a = a
1 · a = a
Distribución:
a · (b +c) = a · b + a · c
Se entiende por puertas lógicas los dispositivos básicos sobre los cuales se puede diseñar un sistema digital. Éstas solo tienen una única salida, aunque pueden tener una o más entradas. Las puertas lógicas a la salida pueden dar niveles de tensión alto (1) o niveles de tensión bajo (0).
En estos dispositivos hay que tener en cuenta que dependiendo de la tecnología del fabricante de los circuitos (TTL y CMOS) varían los niveles de tensión en las entradas y en las salidas. Esto hay que tenerlo en cuenta ya que en la electrónica digital lo que se pretende es enviar la información más fiable posible. Por ejemplo el voltaje de alimentación de las puertas TTL es de 5 V, mientras que el de las puertas CMOS varía entre 3 y 15V.
A continuación veremos las puertas lógicas básicas que son: OR, NOR, AND, NAND, NOT, EX-OR, y EX-NOR.
| Función | Dibujo esquemático |
| S = a + b | 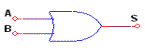 |
| a | b | S |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
| Función | Dibujo esquemático |
| ______ |
|
| S = a + b |
| a | b | S |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
| Función | Dibujo esquemático |
| S = a · b |
| a | b | S |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
| Función | Dibujo esquemático |
______ |
|
| S = a · b |
| a | b | S |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
| Función | Dibujo esquemático |
__ |
|
| S = a |
| a | S |
|---|---|
0 |
1 |
1 |
0 |
| Función | Dibujo esquemático |
| S = a |
| a | b | S |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
| Función | Dibujo esquemático |
| S= a |
| a | b | S |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
| Abrir archivo pdf: electronica_digital.pdf |