Tiramos con una fuerza de 150 N de un bloque de masa 10 000 g apoyado en una superficie que forma un ángulo de 10º con la horizontal por medio de una fuerza que forma a su vez con el plano un ángulo de 15º. Si el coeficiente de rozamiento entre el plano y el bloque es 0,6, calcula:

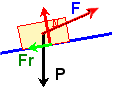
a) El valor de las componentes del peso y de la fuerza. Dibuja sus puntos de aplicación dirección y sentido.

b) El valor de la normal.

c) La fuerza de rozamiento máxima.

a) La aceleración con la que se mueve.

Nota.Toma para g (9,81 m·s^-2 ) el valor de 10 m·s^-2.

Resolución P 7

Datos

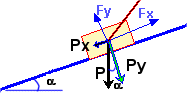
Con el diagrama representamos las fuerzas y las descomponemos en los ejes. Suponemos el cuerpo reducido a un punto sobre el que actúan las fuerzas. Tomamos como eje x (en el que se desplaza) el paralelo al plano.

a)
Peso cuerpo = mg = 10· 9,8 = aprox (g=10) = 100 N

El ángulo que forma P con los ejes es igual al del plano por ser ángulos con lados perpendiculares.

Px = P · sen 10º = 100 · sen 10º =17,36 N
Py = P ·cos10º = 100· cos 10º = 98,48 N

Fx = F · cos 15º = 150· 0,96 =144,88 N

Fy = F· sen 15º =150 ·0,258 = 38,82 N

b)
La componente Py del peso empuja el bloque contra el plano, pero la componente Fy de la fuerza de arrastre disminuye en su valor el empuje Py. Por lo tanto lo que queda de empuje (Py -Fy) es el que origina la normal N.

En el eje vertical: S F y = 0
Py- Fy = N
98,48 - 38,82 = NN = 59,66 N

c)
Fr = 0,6 · N = 35,8 N

d)
En el eje x se ejerce la tracción de arrastre. S F x = m· a

Fx - Px- Fr = m·a
144.88 - 17,36 - 35,8 = 10 · a

La componente del peso y la Fr no neutralizan la fuerza de traccción Fx por lo tanto el bloque acelera en esa dirección.
a = 9,172 m·s^-2