FUNCIONES Y GRÁFICAS

1. CONCEPTO DE FUNCIÓN

Debes recordar que una función es aquella correspondencia que asocia elementos de dos conjuntos numéricos, de manera que a cada elemento del primer conjunto le corresponde uno y solo uno del segundo.

Así, una correspondencia que asocie a cada alumno de esta clase su nota en el Ámbito Científico Técnico, no sería una función ya que los elementos del primer conjunto son personas, no números. Sin embargo, si lo que asociamos es a cada número de lista de los alumnos la nota correspondiente a ese alumno, sí sería una función, ya que ahora los dos conjuntos están formados por números (los números de lista y las notas) y a cada elemento del primer conjunto le corresponde uno y solo uno en el segundo, no puede haber un alumno que tenga dos notas al mismo tiempo.

1. Decide razonadamente , si las siguientes correspondencias son funciones o no. En tu hoja de trabajo deberás justificar las razones por las que se trata de una función o no.

a) A todo número natural se le hace corresponder el natural siguiente.

b) A todo número entero se le hace corresponder su opuesto.

c) A todo número natural se le asocian sus divisores.

d) A todo número positivo se le asocia su raíz cuadrada.

e) A todo número se le asocia su doble más cinco.

2. REPRESENTACIÓN GRÁFICA: LOS PUNTOS:

Sabes que para representar puntos utilizamos un Sistema de Referencia , en el que cada punto viene determinado por un par de números, las coordenadas. El primero de ellos recibe el nombre de abscisa y se representa en el eje horizontal o eje de abscisas. El segundo es la ordenada y se representa en el eje vertical o eje de ordenadas.

1. En la siguiente imagen tienes todos estos elementos. Dibújalos en tu hoja de trabajo.

2. Copia en tu hoja de trabajo y completa la tabla que aparece a continuación, indicando si las coordenadas de los puntos son positivas, negativas o cero. Ayúdate de la siguiente escena para responder al ejercicio.

3. Escribe las coordenadas de los puntos que aparecen en la imagen. Una vez hecho, haz clic en el botón “animar” y escribe las coordenadas de los nuevos puntos generados.

3 LO QUE NOS DICEN LOS PUNTOS

Has visto en las actividades anteriores que para representar puntos utilizamos un Sistema de Referencia, en el que cada punto viene determinado por un par de números, las coordenadas . El primero de ellos, la abscisa , se representa en el eje horizontal o eje de abscisas. El segundo, la ordenada , se representa en el eje vertical o eje de ordenadas.

La posición de los puntos en el sistema de referencia y sus correspondientes coordenadas nos dan información sobre las magnitudes que estas relacionan. En las siguientes actividades aprenderás, al menos eso espero, a interpretarlas. Trata de resolverlas y ayúdate de las imágenes para ello.

1. Observa la imagen que aparece a continuación y los puntos representados en los ejes de coordenadas. ¿Quién está representado por cada punto? (El extraterrestre es el de mayor edad de todos). Dibuja en tu hoja de trabajo la posición de los puntos A, B, C, D, E y F.

2. Una empresa dispone de dos avionetas para el transporte de viajeros, de diferentes características. Las llamaremos A y B.

a. En la siguiente gráfica se relacionan dos de sus características, antigüedad y precio. A partir de ella, ¿podrías decir cuál de los dos aviones es más caro?

b. Si la avioneta B es más grande y también la más rápida, ¿qué punto podría representar a la avioneta B?

c. A partir de la información contenida en las dos gráficas anteriores indica el punto que representa a   la avioneta A en los siguientes ejes.

3. A partir de la gráfica dibujada a continuación, señala a quién crees que corresponden los puntos en ella dibujados.

(1) Si no fuera por que es un vago, sacaría mejores notas.

(2) Ha trabajado mucho, pero no ha tenido suerte en el examen.

(3) Ha visto muy bien recompensado su esfuerzo.

(4) A éste se le ha aparecido la Virgen.

4 Interpretando GrÁficas

En las siguientes actividades aprenderemos a leer la información que nos pueden mostrar las gráficas de una función.

1. La siguiente gráfica muestra la temperatura registrada en un observatorio meteorológico durante las 24 horas de un día de invierno. Ayudándote de la escena que aparece a continuación, contesta a las siguientes preguntas:

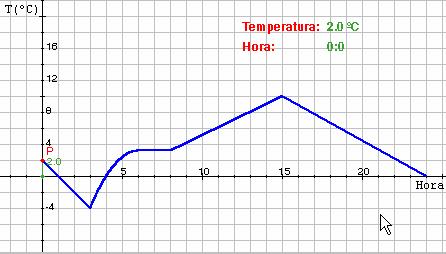
a. ¿A qué horas se produjeron las temperaturas máxima y mínima de ese día?

 

b. ¿Cuáles son los intervalos de tiempo en los que la temperatura aumenta?

 

c. ¿Existe algún periodo de tiempo en el que la temperatura se mantenga constante?

 

d. ¿A que horas la temperatura es de 0 ºC ? ¿Y de 4 ºC ?

2. La siguiente gráfica muestra la distancia en kilómetros recorrida por un ciclista que inicia su excursión a las 8 de la mañana y la termina cuando regresa al punto de partida.

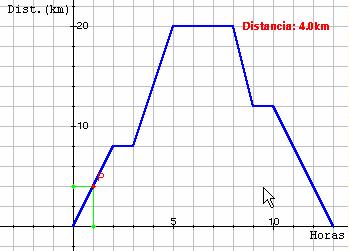
a. ¿Cuánto a durado la excursión? ¿A qué hora se terminó?

 

b. ¿Cuántos kilómetros ha recorrido en total?

 

 

c. ¿Durante cuánto tiempo no aumenta la distancia recorrida y, por lo tanto, podemos considerar que está parado?

d. ¿Qué distancia recorre entre las 11 de la mañana y la una de la tarde?

 

e. ¿Sabrías calcular la velocidad a la que se ha movido en ese trozo de su excursión?

 

En la siguiente actividad nos vamos a centrar en esa parte de la excursión, la que transcurre entre las 11 de la mañana y la una de la tarde. Para ello, en la siguiente escena, tienes dibujada solo esa parte de la gráfica. Se trata de que descubras cómo teóricas velocidades diferentes influyen en la inclinación de segmento correspondiente de la gráfica.

3. La velocidad la calculamos dividiendo el espacio recorrido entre el tiempo empleado en recorrerlo. Introduce diferentes valores para el tiempo empleado en recorrer esos 12 kms (en el campo " tiempo empleado ") y anota la velocidad que llevaría el excursionista y los efectos gráficos que se producen.

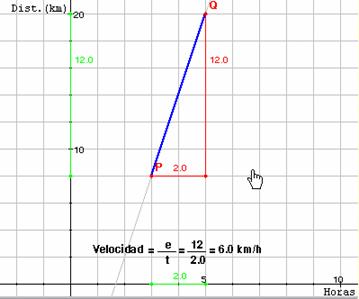
Has visto que cuanto mayor es la velocidad más inclinación tiene ese segmento. En este caso hablamos de velocidad puesto que estamos viendo como varía el espacio con relación al tiempo , trabajamos con las variables espacio y tiempo, en Matemáticas cuando se trabaja con las variables y y x , hablamos de pendiente , ya que nos mide la pendiente o inclinación.

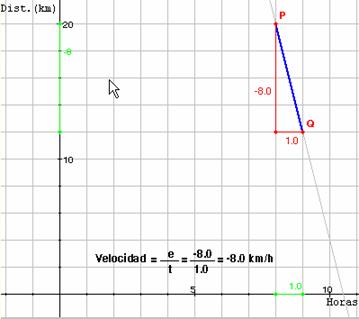
En la siguiente actividad, nos centraremos en otra parte de la excursión, cuando inicia su regreso, es decir entre las 16 y las 17 horas. En la siguiente escena se determina la velocidad que lleva en ese intervalo de tiempo en el que la distancia al punto de partida de la excursión va disminuyendo.

4. Cambia el tiempo empleado en ese trayecto y anota la correspondiente velocidad del excursionista y sus efectos sobre la gráfica. ¿Qué significado crees que tiene que la velocidad tome en este caso valores negativos?

Hay otras formas de describir una función, mediante una tabla de valores y por medio de una fórmula que relacione ambas variables. En la siguiente actividad deberás, a partir de la gráfica construir una tabla de valores para la función y tratar de encontrar su fórmula o ecuación .

5. La escena siguiente representa una función que nos indica el número de piezas (y) que produce una determinada máquina en función del tiempo en minutos (x).

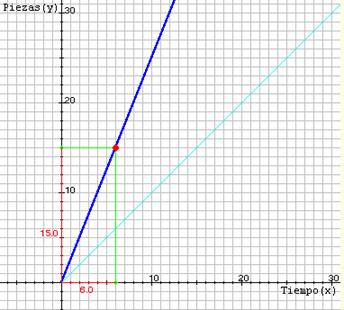
a. Con la ayuda de la escena copia y completa, en tu hoja de trabajo, la siguiente tabla de valores:

b. ¿Cuántas piezas produce esta máquina cada minuto?

 

c. Trata de encontrar la fórmula que relaciona el número de piezas fabricadas con el tiempo empleado en fabricarlas.

En la siguiente actividad volvemos a insistir sobre la creación de una tabla de valores y la búsqueda de la expresión matemática que relacione las dos variables que en ella intervienen. Este problema es un poco más complicado. Como observarás en la escena, la gráfica que lo representa es una curva llamada parábola . Trata de encontrar las soluciones a las preguntas que se te plantean por tí mismo pero, si no lo consigues, no te preocupes, la escena te ayudará a encontrarlas.

6. Un ganadero de ovejas posee una gran finca de pasto. Desea que sus ovejas pasten en lugares fijos de la finca, para ello, construye zonas de pastoreo rectangulares con un vallado móvil de 60 m de longitud. La superficie de pastoreo dependerá de la anchura de la zona vallada. (Recuerda que la superficie de un rectángulo es "ancho x largo".

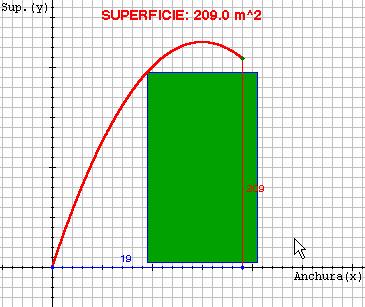
a. Completa la siguiente tabla de valores, ayúdate de la escena (variando los valores de la anchura, x,) si es necesario.

b. Encuentra la expresión matemática que relaciona la anchura (x) de del recinto con la superficie del mismo (y).

c. ¿Qué dimensiones debe tener la zona de pastoreo para que sea máxima su superficie? ¿A qué figura correspondería?