

INFORME FINAL
I. Descripción de la situación inicial
I.1. GRUPO:
Datos:
- Nivel de 3º de ESO
- Grupo de 12 alumnos (3 chicos, 9 chicas).
- IES Salvaterra de Miño, en Salvaterra de Miño (Pontevedra)
Características generales:
- Curso con buen ambiente de trabajo
- 50% de aprobados en la primera evaluación, con algunas notas altas, y ningún suspenso inferior a 3.
- Instituto localizado en una comarca rural, de interior, pero bien comunicada (con Portugal, la costa atlántica, la ciudad de Vigo).
I.2. OBJETIVOS:
- Afianciación del lenguaje algebraico como forma de expresión de realidades geométricas.
- Interpretar los polinomios como fórmulas asociadas a situaciones geométricas.
- Relacionar e interpretar el valor numérico de un polinomio.
- Deducir fórmulas a partir de situaciones geométricas.
I.3. CONTENIDOS:
- Operaciones con polinomios, suma y multiplicación.
- Valor numérico de un polinomio: concepto y cálculo.
- Los polinomios como fórmulas que representan áreas de polígonos.
- Identidades notables: cálculo e interpretación geométrica.
- Adquisición de destrezas del lenguaje algebraico.
I.4 MATERIALES:
-Cuaderno de clase.
-Calculadora.
-Ordenadores: dispusimos de 6 ordenadores, uno para cada dos alumnos, con sistema operativo Windows 98, y procesador pentium II o III.
I.5 TEMPORALIZACIÓN:
- La experiencia se ha llevado a cabo a principios del segundo trimestre, a la vuelta de las vacaciones navideñas.
- Tras una semana (3 sesiones de 50') de clases introductorias, repasando los conceptos y operaciones básicas de monomios y polinomios comenzó el trabajo con el ordenador.
- Los alumnos tienen clase de matemáticas lunes, martes y viernes, y el aula de informática estaba libre los martes y los viernes, por lo que disponíamos de 2 días a la semana para acudir a ella.
- Las sesiones en el aula de informática fueron 5, distribuidas en 3 semanas, a razón de dos sesiones por semana excepto la primera, donde coincidía un día festivo.
-Tras el trabajo en el aula de informática se dedicó una sesión a realizar la prueba de conocimientos, y otra a comentar los resultados y llevar a cabo las encuestas.
CALENDARIO:
| LUNES | MARTES | VIERNES |
| 26-enero: clase en el aula ordinaria sobre operaciones con polinomios. | 27-enero: 1ª sesión en el aula de informática | 30-enero: festivo |
| 2-febrero: clase teórica sobre identidades notables | 3-febrero: 2ª sesión el el aula de informática | 6-febrero: 3ª sesión el el aula de informática |
| 9-febrero: clase práctica sobre identidades notables | 10-febrero: 4ª sesión el el aula de informática | 13-febrero: 5ª sesión el el aula de informática |
| 16-febrero: prueba escrita de conocimientos. | 17-febrero: encuestas. |
I.6 LOCALIZACIÓN:
- Las sesiones teóricas se llevaron a cabo en el aula ordinaria, y las prácticas en el aula de informática del IES.
- El aula de informática es amplia, y cuenta con 16 ordenadores, conectados a internet y en red local. Se instaló el Descartes y la correspondiente actividad en 6 de los ordenadores, de manera que los alumnos trabajaran por parejas.
II. Descripción del desarrollo
II.1 Actitud de los alumnos:
De una postura inicial del tipo "qué bien, vamos al aula de informática a jugar con los ordenadores", se pasó por otra más perezosa al darse cuenta de que era un trabajo serio (tener que leer el texto de las actividades, tener que escribir los ejercicios en el cuaderno, distraerse con el compañero...), hasta llegar a una última fase más satisfactoria: dominaban el manejo de las escenas, entendían los ejercicios (no eran tan difíciles como parecían inicialmente), les entretenían, y estaban motivados para conseguir hacerlos.
II.2 Incidencias y problemas:
No hubo grandes incidencias que reseñar, los ordenadores a veces cargaban mal las escenas, pero con un "actualizar" se solucionaba el problema. Las mayores dificultades que encontraban los alumnos se debían a su falta de costumbre para "leer comprensivamente" (o simplemente pereza, falta de atención) un texto matemático, sin contar con la ayuda del profesor que lo explique, con lo que a casi todos los grupos tuve que explicarles, oralmente, lo que había que hacer en cada escena. Este problema disminuyó los últimos días, dando la impresión de que conforme estaban más metidos en el manejo del programa (y puesto que, a fin de cuentas, todas las actividades explotaban el mismo concepto, la relación entre polinomios y áreas), ya no necesitaban de la explicación oral. En cuanto a actividades concretas, retiré el apartado de la actividad IV sobre identidades notables que pedía explicar, gráficamente, las fórmulas (a-b)^2 y (a-b)*(a+b). Me di cuenta, con los primeros grupos que llegaron a ella, que la explicación gráfica les resultaba complicada, al ser, no una división de un polígono en trozos, como el caso de (a+b)^2 y de la actividad 3.2 que habían resuelto antes, si no una resta de trozos poco natural. De hecho, creo que de haberla hecho después de las actividades V y VI, donde sí ya manejaron con soltura sumas y restas de fragmentos de polígonos, les habría sido más fácil.
III. Resultados
Se adjuntan los ficheros .PDF con las preguntas de la prueba de control de conocimientos, y las dos encuestas, a los cuales también se puede acceder mediante los links situados a continuación.
Estadísticas de la corrección de actividades y la prueba de conocimientos
prueba objetiva, archivo: exdescartes.pdf
| Alumno | Actividades | Prueba |
| 1 | 5 | 3 |
| 2 | 5 | 4,25 |
| 3 | 5,25 | 4,75 |
| 4 | 5,5 | 4,75 |
| 5 | 6 | 4,75 |
| 6 | 6 | 5 |
| 7 | 6 | 6,75 |
| 8 | 6 | 7,5 |
| 9 | 6 | 7,75 |
| 10 | 8,25 | 8 |
| 11 | 9,5 | 9,5 |
| 12 | 9,75 | 9,5 |
| Media | 6,52 | 6,29 |
| Moda | 6 | 4,75 |
| Mediana | 6 | 5,88 |
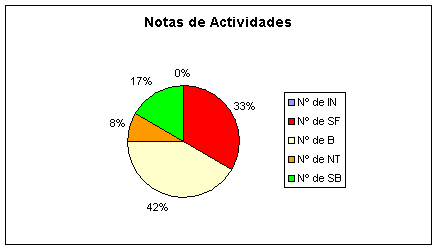
| ACTIVIDADES | PRUEBA |
 |
|||
| Nº de IN | 0 | 0% | 2 | 17% | |
| Nº de SF | 4 | 33% | 4 | 33% | |
| Nº de B | 5 | 42% | 1 | 8% | |
| Nº de NT | 1 | 8% | 3 | 25% | |
| Nº de SB | 2 | 17% | 2 | 17% | |
| Nº de aprobados | 12 | 100% | 10 | 83% | |
| Nº de presentados | 12 | 12 | |||
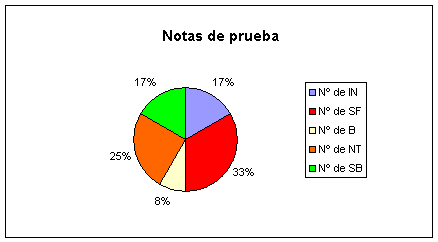
| PRUEBA |
 |
|||
| Intervalos de notas | f. acum. | f. abs. | f.rel. | |
| [0,3) | 0 | 0 | 0% | |
| [3,5) | 5 | 5 | 42% | |
| [5,6) | 6 | 1 | 8% | |
| [6,7) | 7 | 1 | 8% | |
| [7,8.5) | 10 | 3 | 25% | |
| [8.5,10] | 12 | 2 | 17% | |
| Nº de datos | 12 | |||
Comentarios: En general los resultados son positivos, el porcentaje de aprobados es bastante superior al de la evaluación, y excepto una persona, las notas de los suspensos son altas (de hecho, 4.75 se ha considerado aprobado). Las personas que destacan en la clase, como alumnos de sobresaliente, siguen siendo las mismas, pero hay una nota media mejor. Por supuesto, la prueba era sencilla, y sobre una cantidad de materia pequeña. En general, puede decirse que los alumnos han aprendido a asociar un polinomio a un polígono, y en ambas direcciones (tanto obtener el polinomio, dado el polígono, como lo contrario), aunque después comentan errores a la hora de resolver un ejercicio concreto. Sin embargo, y a la vista concreta de los exámenes, la relación entre el valor numérico y el área para un tamaño particular de polígono no parece haberles quedado, en general, tan clara. En cuanto a las actividades, las notas bajas se deben básicamente a errores en algunos de los apartados y al poco cuidado en tomar nota en la libreta de las mismas.
Estadísticas de las encuestas, abierta y cerrada
encuestas realizadas a los alumnos, archivo: encuestadescartes.pdf
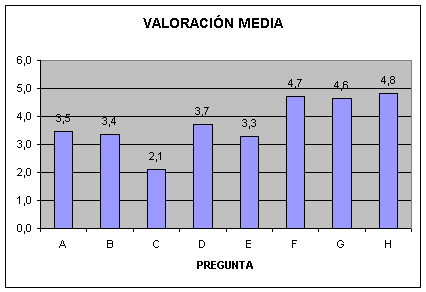
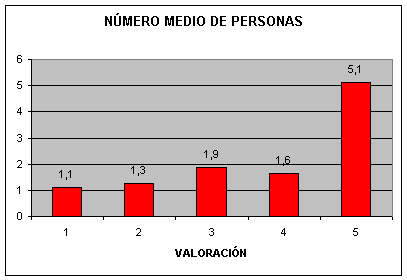
| FRECUENCIA VALORACIÓN |
 |
||||||
|---|---|---|---|---|---|---|---|
| ENCUESTA CERRADA | 1 | 2 | 3 | 4 | 5 | nota media de la pregunta | |
| A | 1 | 1 | 3 | 4 | 2 | 3,5 | |
| A | 9,1% | 9,1% | 27,3% | 36,4% | 18,2% | ||
| B | 0 | 4 | 1 | 4 | 2 | 3,4 | |
| B | 0% | 36% | 9% | 36% | 18% | ||
| C | 5 | 2 | 3 | 0 | 1 | 2,1 | |
| C | 45% | 18% | 27% | 0% | 9% | ||
| D | 0 | 2 | 3 | 2 | 4 | 3,7 | |
| D | 0% | 18% | 27% | 18% | 36% | ||
| E | 3 | 0 | 3 | 1 | 4 | 3,3 | |
| E | 27% | 0% | 27% | 9% | 36% | ||
| F | 0 | 1 | 0 | 0 | 10 | 4,7 | |
| F | 0% | 9% | 0% | 0% | 91% | ||
| G | 0 | 0 | 1 | 2 | 8 | 4,6 | |
| G | 0% | 0% | 9% | 18% | 73% | ||
| H | 0 | 0 | 1 | 0 | 10 | 4,8 | |
| H | 0% | 0% | 9% | 0% | 91% | ||
| nº medio de personas con esa valoración | 1,1 | 1,3 | 1,9 | 1,6 | 5,1 | 3,8 | |
| ENCUESTA ABIERTA | POSITIVO | NEGATIVO |
 |
| A | usar el ordenador, último ejercicio, y aprender con ordenador | copiar en la libreta, ejercicios teóricos | |
| B | no cambiaría nada | usar la libreta, menos ejercicios, más juegos | |
| C | fácil el último ejercicio | difícil el cálculo de áreas, el hacer dibujos | |
| D | algo nuevo, buena impresión, más fácil de entender | nada |
Comentarios: En los resultados de las encuestas se aprecia que los alumnos no son demasiado críticos. A pesar de sus dificultades iniciales, no las reconocen (o ya no las recuerdan!), y se muestran encantados con trabajar en el aula de informática, con el ordenador, y salir de la monotonía de las clases tradicionales. Es decir, la mayoría destaca el aspecto lúdico. Eso sí, se muestran divididos sobre si realmente las matemáticas así son o no más fáciles, con lo que implícitamente reconocen las dificultades que han tenido.
IV. Valoración personal
Aspectos positivos:
Me ha gustado ver cómo los alumnos han ido, poco a poco, metiéndose en la actividad, pasando de una actitud en principio negativa o pasiva (al ver que no era sencillamente un juego) a otra de cooperación en el grupo, concentración en la actividad, en lo que el texto proponía, etc. En resumen, creo que para ellos también resulta complicado vencer la inercia del método de trabajo tradicional en una clase de matemáticas: atender a una explicación oral y después trabajar, individualmente, en los ejercicios que sobre la explicación se proponen. Les cuesta vencer la ecuación ordenador = juego o trabajo en grupo = diversión, relajo, "actividad no seria".
En cuanto a mi, como profesor ha sido motivante el realizar yo la actividad, proponérsela luego a ellos, y ver cómo respondían, qué les resultaba más fácil o más difícil. Creo, además, que en conceptos donde haya una parte gráfica o geométrica el verlo y manipularlo, como están haciendo con las pantallas de Descartes, les ayuda mucho, rebajando un poco el carácter abstracto de la materia.
Aspectos negativos:
Hay un aspecto negativo fundamental, y es el tiempo. Esta forma de aprender requiere más tiempo que una clase tradicional y con 3 sesiones de 50 minutos a la semana, el programa de 3º de ESO queda enorme... De las cinco sesiones que yo programé en el aula de informática, creo que sólo las dos últimas resultaron productivas (desde el punto de vista del tiempo empleado y los conceptos adquiridos), pues no fue hasta la cuarta sesión que los alumnos empezaron a encontrarse seguros en el manejo del ordenador, a coger el ritmo de las actividades, etc., como comenté más arriba. Pero si realmente se quiere que el trabajo con el ordenador fructifique, hace falta el tiempo, y desde luego, si una cosa me ha quedado clara, es que una o dos sesiones aisladas son insuficientes, y que hace falta una continuidad para que el proceso de aprendizaje se lleve a cabo.
Por lo mismo, hay un cierto riesgo de que el alumno se quede en la parte anecdótica (qué divertido es el ordenador, mover botoncitos...) porque no pueda librarse de la idea preconcebida de que esto no es un trabajo serio, y de que valore la actividad no en función de lo que aprenda o entienda, si no de su carácter lúdico. (Por ejemplo, a muchos alumnos les gustó sobre todo la actividad VI, porque se formaban los polígonos en la pantalla, porque no había que hacer cuentas...)
|
|||||||||||||||