Informe
3º
ESO-A. IES "Cañada de las fuentes" Quesada (Jaén)
-
Conocer los distintos números.
-
Representar los números fraccionarios en la recta real.
-
Expresar un número racional en forma decimal.
-
Obtener la fracción generatriz de un número decimal.
-
Representar en la recta real la raíz cuadrada de un número.
-
Conocer y expresar los intervalos de números reales de distintas
formas.
-
Aproximar números reales mediante truncamiento y redondeo.
-
Obtener una aproximación por redondeo y truncamiento de un
número racional.
-
Hallar el error absoluto y relativo de una aproximación
-
Conocer la historia de la aproximación de Pi.
-
Hallar el error de las aproximaciones.
-
Hallar aproximaciones de Pi por defecto y por exceso.
-
Tipos de números
-
Números racionales. Representación.
-
Expresión decimal de una fracción.
-
Fracción Generatriz.
-
Números irracionales.
-
Números Reales.
-
Intervalos.
-
Aproximaciones.
-
Error absoluto y relativo.
-
Aproximación del número Pi.
Ordenadores
y el programa Descartes:
Unidades: Números Racionales.
Aproximaciones y Aproximación de Pi mediante el
método de Arquímedes.
Aula
de informática con un ordenador para cada pareja de alumnos.
1ª sesión:
Unidad: Números Racionales. Aproximaciones.
1.Tipos de números.
2.Ejercicios.
3.Números Racionales.
4. Representación de números Racionales
5.Ejercicios.
2ª sesión:
Unidad: Números Racionales. Aproximaciones.
5.Expresión decimal de una fracción
6.Ejercicios
7.Función Generatriz
8.Ejercicios
3ª sesión:
Unidad: Números Racionales. Aproximaciones.
9.Números Irracionales.
10.Ejercicios.
11.Números Reales.
12. Orden en R.
13.Ejercicios.
4ª sesión:
Unidad: Números Racionales. Aproximaciones.
14. Intervalos.
15. Ejercicios.
16. Aproximaciones.
17. Redondeo.
18. Ejercicios.
19.Error absoluto.
20.Error relativo.
21.Ejercicios.
5ª sesión:
Unidad: Aproximación de Pi mediante el método de Arquímedes
1.Introducción.
2.Aproximaciones de la historia.
3.Aproximación por defecto.
4.Aproximación por exceso.
Otro planteamiento alternativo sería para un grupo de 4º ESO opción b, con el tema de trigonometría. Primero se trabajaría con la unidad "Razones trigonométricas" y luego "la aproximación de Pi mediante el método de Arquímedes".
Herramientas
de evaluación del desarrollo de la experiencia:
Al
principio los alumnos no quieren trabajar. Quieren jugar o
chatear. Tengo que controlar que estén trabajando en Descartes y
que al final de la sesión me entreguen los ejercicios resueltos.
Una vez que empiezan les gusta.
Algunos
alumnos les parece muy fácil y otros tienes que ir explicando lo
que tienen que hacer.
Después
de cada sesión de Descartes se realiza otra sesión en pizarra
para seguir practicando.
1ª
sesión:
Los
alumnos no conocen "Descartes" y tengo que ir guiándoles
hasta llegar a la página. Tengo que ir explicando que tienen que
hacer grupo por grupo.
Los
alumnos casi que no leen la parte teórica pensando que ya lo
saben de otros años pero al hacer los ejercicios se encuentran
con errores. Después de hacer unos 5 ejercicios ya lo comprenden.
La representación de los números racionales les cuesta pero lo
comprenden y resuelven los ejercicios sin problemas.
2ª
sesión:
Pasar
a la expresión decimal no tienen ningún problema, pero al
contrario los alumnos encuentran dificultades.
3ª
sesión:
La
representación de los números irracionales es lo más
complicado para ellos, pero al final la gran mayoría lo entiende.
Pero al día siguiente ya se le ha olvidado. Algunos les cuesta
arrastrar el punto. Y el ejercicio final hay que explicarlo grupo
por grupo.
4ª
sesión:
Los
intervalos y las aproximaciones los entienden bien. No tienen ningún
problema.
5ª
sesión:
Algunos
alumnos se interesan por la historia y se nota que les gusta. Lo
encuentran interesante. Al ser alumnos de 3º de ESO no les
explico la aplicación trigonométrica.
El
número de aprobados ha aumentado ligeramente con respecto de las
otras pruebas. Los alumnos cometen errores de cálculo y otros
confunden conceptos. Falta que trabajen más en casa.
Hay
que prometerles a los alumnos que tienen un positivo si trabajan
y hacen los ejercicios. Una vez que empiezan, la actividad se
desarrolla con normalidad.
El
control de este tema se ha realizado como los otros, es decir, un
examen escrito. Los resultados obtenidos son:
4
insuficientes, 9 aprobados, 6 bienes, 4 notables, 5
sobresalientes
La
mayoría de los alumnos han mejorado su nota.
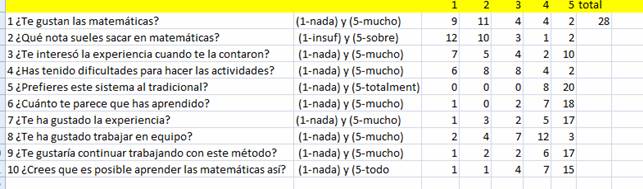
Encuesta:

| 1
¿Te gustan las matemáticas?
|
| 2
¿Qué nota sueles sacar en matemáticas?
|
| 3
¿Te interesó la experiencia cuando te la contaron?
|
| 4
¿Has tenido dificultades para hacer las actividades?
|
5
¿Prefieres este sistema al tradicional?
|
| 6
¿Cuánto te parece que has aprendido?
|
| 7
¿Te ha gustado la experiencia?
|
| 8
¿Te ha gustado trabajar en equipo?
|
| 9
¿Te gustaría continuar trabajando con este método?
|
| 10
¿Crees que es posible aprender las matemáticas así?
|
La
encuesta abierta no ha aportado ninguna información.
La
actividad me parece que es positiva aunque hay que estar
continuamente vigilándolos para que estén trabajando. Los
alumnos trabajan porque tienen que entregar los ejercicios
resueltos. Los alumnos se implican, aunque hay que darles un
margen. Cuando el ejercicio es muy fácil, se sienten un poco
ofendidos y cuando es difícil no lo quieren hacer. Está bien
para mezclar con las clases con pizarra. Algunos se motivan y
otros encuentran otra página web para cuando tengan dudas.
El
aspecto negativo es cuando los alumnos no quieren hacer nada y se
dedican a molestar o a navegar por otras páginas. Y tener
cuidado de que no deterioren los ordenadores.
En
general los alumnos se motivan más porque parece que no tienen
que trabajar tanto y es más ameno hacerlo con los ordenadores.
Por otro lado estamos en la era de la información y la
informática. Los alumnos están mucho tiempo con el ordenador ya
sea jugando o trabajando, y aprenden que se puede trabajar
matemáticas con el ordenador. Además, hay que fomentar que
aprendan a utilizar el ordenador para el estudio, ya que es el
medio de comunicación más utilizado actualmente.
| Milagros Rodríguez Saeta | |
 |
|
| © Ministerio de Educación, Política Social y Deporte. Año 2008 | |