|
|
|
| Agustí Estévez Andreu | |
|
|
|
| ÍNDICE | |
|
2. Desarrollo 3. Resultados |
|
La experiencia que se ha llevado a cabo como proyecto del curso Descartes 2.0, se ha realizado en la Escuela Santíssima Trinitat, de Barcelona. Contamos con un aula de informática para 35 alumnos/as, otra para 30 y una tercera, como aula de Tecnología, con 15 ordenadores. Además, disponemos de una PDI fija y dos portátiles, así como de proyectores y ordenadores portátiles.
El material que se ha desarrollado con Descartes 2 es sobre el tema de la programación lineal. El motivo por el cual se ha elegido el tema es porque lo publicado hasta el momento no correspondía a las necesidades de nuestra programación de asignatura y, en segundo lugar, por ser el contenido que correspondía al grupo escogido.
El grupo seleccionado para llevar a cabo el experimento ha sido el de 2º de Bachillerato de Humanidades y Ciencias Sociales. Está formado por 23 alumnas y alumnos. El nivel de conocimientos no es demasiado alto, muestran poca dedicación a la asignatura y, en la mayoría de casos, los estudios que realizarán el próximo curso no estarán relacionados, al menos explícitamente, con la Matemática. El curso pasado ya habían trabajo con materiales Descartes, en los temas de Estadística y Probabilidad, por lo que han tenido relación con las escenas.
Los objetivos, extraidos de la programación de la asignatura, son:
- Aplicar los conceptos y procedimientos aprendidos a diferentes ámbitos de las Ciencias Sociales, resolviendo situaciones problema que muestren la interconexión de las diferentes partes de la Matemática.
- Saber representar un modelo matemático de programación lineal, aplicarlos a la vida cotidiana y extraer conclusiones
- Usar las herramientas tecnológicas para resolver problemas, ahorrando cálculos y facilitando la visualización.
- Reconocer diferentes tipos de razonamiento.
- Consolidar la idea de que las Matemáticas son un buen instrumento para la aplicación del método científico, explorando situaciones que comporten planificación, experimentación, formulación de conjeturas y su consolidacion.
- Saber controlar los posibles errores en las aplicaciones de los nuevos procedimientos aprendidos.
- Incorporar la vocabulario elementos propios del lenguaje matemático para transmitir mensajes en contextos en los que sea especialmente necesaria la comunicación científica.
- Puntos y vectores del plano. Coordenadas de un punto.
- Ecuación de la recta.
- Posiciones relativas de rectas. Incidencia y paralelismo.
- Sistemes de ecuaciones lineales con dos incógnitas.
- Inecuaciones y sistemas de inecuaciones lineales con dos incógnitas.
- Problemas de progración lineal con dos variables.
- Representación de la región factible.
- Cálculo de la solución óptima.
- Matemática: desarrollar y aplicar el razonamiento matemático para resolver problemas en situaciones diversas.
- en Modelización: interpretar matemáticamente una determinada situación para conocer su comportamiento y controlarla.
- en Proactividad: alcanzar la capacidad para planificar, organizar el trabajo y trabajar en equipo. Aprender a tomar decisiones con espíritu crítico y visión global.
- en Contextualización: interpretar la realidad social a partir del conocimiento matemático propio y explicar estas realidades.
- en Investigación: experimentar, observar, establecer hipótesis i buscar argumentos que la validen o refuten.
- Comunicativa.
- en Gestión y tratamiento de la información.
- Digital.
- en Conocimiento e interacción con el mundo.
- 23 ordenadores con conexión a internet de banda ancha, uno por alumno/a
- proyector, para las explicaciones iniciales sobre el funcionamiento de las escenas.
Esta práctica se ha llevado a cabo en una de las aulas de informática de la escuela, en la que hay instalado un proyector y una PDI portátil, además de en el aula del grupo, en la que no hay recursos TIC fijos.
La experiencia no se ha considerado de forma aislada, como el proyecto de curso Descartes 2, sino que se ha integrado en la programación de la asignatura, dentro del tema de programación lineal. El desarrollo es el siguiente:
- 8 sesiones (2 semanas) en el aula del grupo
- desarrollo de la primera parte del tema, en la que se introducen los conceptos del tema y se resuelven inecuaciones y sistemas de inecuaciones lineales mediante el método tradicional.
- 1 sesión en el aula de informática con una PDI portátil
- ubicación y modo de acceso a los materiales.
- explicación de cómo se desarrollará la experiencia dentro y fuera del aula de informática.
- explicación de cómo se integrará esta práctica en la evaluación de la materia.
- los alumnos deberán contestar a determinadas preguntas (indicadas en las diferentes actividades) en su cuaderno, escanear estas páginas y enviarlas a una tarea del aula virtual de la escuela (moodle). Esta tarea corresponde al bloque de pruebas de clase, al que el departamento tiene asignado un 20% de la nota trimestral de la materia.
- se
realizará un examen tradicional para conocer si los contenidos han sido
asimilados, así como las competencias que se han trabajado.
- explicación de cómo instalar Descartes.
- recordatorio de cómo utilitzar una escena Descartes (controles, ....).
- explicación de cómo utilizar los materiales.
- 5 sesiones en el aula de informática: realización de las actividades usando el material Descartes diseñado.
- 2 sesiones para cada una de las dos primeras páginas.
- 1 sesión para la tercera.
- 2 sesiones en el aula del grupo
- planteamiento de problemas de programación lineal y resolución por el método tradicional.
- explicación de cómo utilizaremos los materiales Descartes para resolver estos problemas.
- 1 sesión en el aula de informática
- para resolver con la última escena Descartes los problemas planteados en las 2 sesiones anteriores.
- analizar los inconvenientes de la resolución gráfica con lápiz y papel y hacer ver la necesidad de buscar resultados que minimicen el riesgo de cometer errores.
Diario del profesor:
La
mayoría de los problemas experimentados por los alumnos se debían a no
entender con exactitud lo que las actividades pedían. Pero a partir de
la 2ª sesión, estas dificultades disminuyeron, pues se trataba de
adaptarse a una nueva manera de trabajar. Al principio, pensaban que de
todas las actividades debían hacer algo en su cuaderno. En cuanto
entendieron la filosofía de trabajo, se sintieron más cómodos y muchas
dudas desaparecieron.
Algún grupo, como después se manifiesta en
algunas cuestiones, está aún lejos de comprender que esta nueva forma
de trabajar necesita mayor implicación por su parte. Ya no son parte
pasiva, como en el método tradicional, sino que participan activamente
de su aprendizaje. Con más tiempo siguiendo esta línea de trabajo
seguramente entenderían este nuevo paradigma.
Otras
dificultades, mayoritarias, han estado relacionadas con la parte más
algebraica, en la que de la región se había de hallar el sistema de
inecuaciones. El hecho de que el alumno obtuviera una inecuación o una
desigualdad diferente a la de la escena, le provocaba un conflicto del
que le era difícil salir. No se daba cuenta de que el resultado era
equivalente, ya que, o bien cambiaban los signos de los términos de la
inecuación, o bien el tipo de inecuación era diferente (explícita,
implícita, ....). Estos errores corresponden más a la competencia
matemática que al material diseñado. Aun así, se podría añadir alguna
información al respecto en la página.
Un aspecto muy positivo
observado es que es más fácil conocer, y por tanto poder llegar a evaluar,
las actitudes de los alumnos ante la asignatura. También, como ya no se
dedican únicamente a copiar de la pizarra y a, esporádicamente,
plantear sus dudas al profesor, se ven más sus capacidades frente a
situaciones problemáticas.
Control de los conocimientos:
El examen de control que se pasó a los alumnos se puede descargar clicando en la imagen siguiente.
Los resultados, número de alumnos que obtienen una calificación de 0 a 10, agrupadas éstas en intervalos de longitud 1, se muestran a continuación. Para un mejor análisis se podría crear un grupo de control, pero en nuestra escuela no es posible, ya que sólo tenemos un grupo del nivel escogido. Tampoco es posible compararlo con grupos de cursos anteriores, ya que éste tiene un nivel académico bastante inferior.
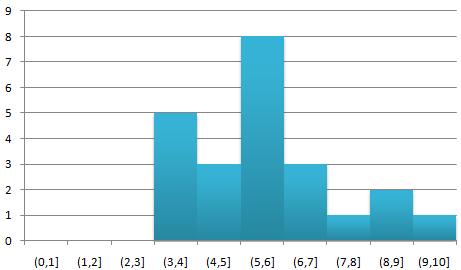
Como elemento de comparación se han seleccionado las calificaciones obtenidas por estos mismos alumnos/as en una prueba similar, en el primer trimestre, sobre álgebra lineal:
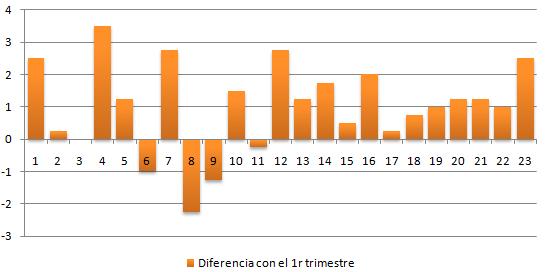
En esta última, se puede comprobar que sólo 4 alumnos obtiene peores calificaciones, es decir, que mejoran su nota aproximadamente un 83%. Este análisis se tiene que tomar con precaución, debido al sesgo entre ambas pruebas.
Encuestas realizada a los alumnos:
- Encuesta cerrada:
Nº |
Pregunta |
|
1 |
¿Te gustan las
Matemáticas? (1-nada, 5-mucho) |
|
2 |
¿Qué nota sueles
obtener en Matemáticas? (1-insuficient, 5-excelente) |
|
3 |
¿Te interesó la
práctica cuando te la explicaron? (1-nada, 5-mucho) |
|
4 |
¿Has tenido
dificultades para hacer las actividades? (1-muchas, 5-ninguna) |
|
5 |
¿Prefieres este
sistema de aprendizaje al tradicional? (1-nada, 5-totalmente) |
|
6 |
¿Cuánto te parece
que has aprendido con esta práctica? (1-nada, 5-mucho) |
|
7 |
¿Te ha gustado la
experiencia? (1-nada, 5-mucho) |
|
8 |
¿Te ha gustado
trabajar en equipo? (1-nada, 5-mucho) |
|
9 |
¿Te gustaría
continuar trabajando con este método? (1-nada, 5-mucho) |
|
10 |
¿Crees que es
posible aprender Matemáticas con este método? (1-nada, 5-todo) |
- Encuesta abierta:
- Indica qué es lo que más te ha gustado de esta experiencia.
- Indica qué es lo que menos te ha gustado de esta experiencia.
- Indica qué cosas cambiarías y cuáles no.
- Si quieres añadir alguna cosa más sobre las respuestas de la primera parte, hazlo aquí.
- Expresa tu valoración general o los
comentarios que creas que podrían ser de interés para mejorar la
experiencia.
Análisis de los resultados:
De la encuesta cerrada, la primera gráfica representa, por cada una de las 10 preguntas, el porcentaje de alumnos que han asignado un 1, 2, 3, 4 ó 5 puntos.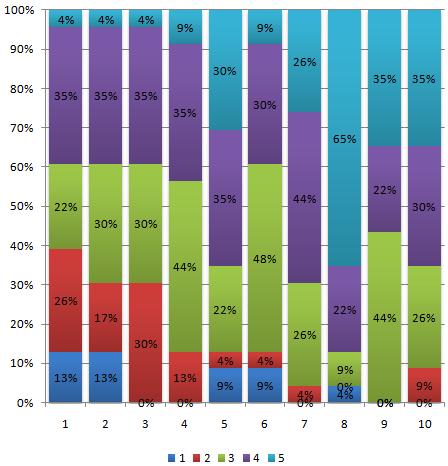
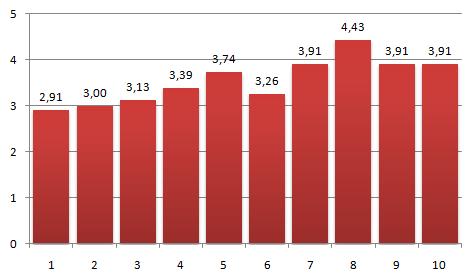
Es habitual que estos grupos no tenga una afinidad con la asignatura, lo que también se percibe en las calificaciones que obtienen (pregunta 1 y 2). Es por ello que, en principio, tampoco muestren excesivo interés por innovar en su enseñanza y aprendizaje (pregunta 3). Sin embargo, es por estos motivos que creo que es el tipo de grupo para los que es más necesario, si cabe, apostar por nuevas técnicas y materiales como los que se han usado en esta experiencia.
La evaluación del material diseñado es positivo, puesto que sólo un 13% ha tenido dificultades para hacer las actividades (pregunta 4), aunque también es verda que casi la mitad (un 44%) puntúa esta pregunta con un 3 (respuesta mediana).
Este tipo de materiales parece tener buena aceptación, como lo demuestra que el 65% prefiera este método al tradicional (pregunta 5). Sin embargo, la percepción de haber aprendido bastante con la práctica es del 39% (pregunta 6). Tal vez este resultado se pueda explicar porque la mayoría de conceptos ya se habían introducido con el método tradicional y a la mayoría de alumnos/as sólo les pareciese una manera de poner en práctica lo aprendido en el aula del grupo. Todo y esto, un 65% cree que es posible aprender con estos materiales (pregunta 10).
Finalmente, en lo que podría ser la motivación del alumnado, los resultados son muy positivos, destacando la excelente acogida que supone el trabajo en grupo, cosa que acepta de buen grado el 87% (pregunta 8). También la continuación de este método tendría aceptación, ya que al 70% le ha gustado bastante la experiencia y a un 57% le gustaría repetirla en el futuro (preguntas 7 y 9).
Otros aspectos que destacan los alumnos/as son los siguientes:
- La posibilidad de modificar valores, mover puntos y rectas, ...
- El entorno gráfico favorece la comprensión de algunos conceptos.
- Manera más rapida de hacer cosas rutinarios: dibujar rectas, regiones, ...
- Ambiente diferente que sale de lo cotidiano.
- Trabajar en equipo y ayudarnos entre todos.
- Se debería combinar este método con el tradicional.
- En algunos ejercicios se necesitarían más explicaciones.
- En algunos casos comentan que puede provocar distracciones.
- Algunos alumnos/as quisieran poder poner las respuestas en la misma página y no en otro documento.
- Ven difícil aplicar el método en temas que no sean gráficos.
- Muchos/as hacen referencia a que dónde de verdad se aprende es en la pizarra.
- La dificultad para tomar apuntes.
Como aspectos negativos, aunque positivos para la mejora de los materiales, la redacción incompleta o de difícil comprensión de los enunciados es bastante recurrente, así como la dependencia del método tradicional (natural debido a que ésta ha sido la esencia de su formación desde, como mínimo, el comienzo de la secundaria).
Mi valoración personal, a tenor de los resultados analizados, es más que positiva, incluso mayor que en otras ocasiones en las que había usado Descartes, también con este grupo. El hecho de haber creado mis propias escenas y enunciados, adaptados a la programación de la asignatura en nuestro centro y al grupo de alumnos, ha sido un factor clave para que me sintiera más cómodo en las sesiones, al saber que los alumnos no se encontrarían con conceptos o actividades que no se hubieran trabajado en cursos anteriores y que hubieran dificultado el progreso de éstos.



