10 FORMA MATRICIAL DE UN SISTEMA

Todo sistema de  m  ecuaciones lineales con  n  incógnitas se puede escribir en forma matricial de la forma A .X = B. 

10.1 MATRIZ AMPLIADA

Es la matriz A* de dimensión  mx(n+1)  que se obtiene a partir de la matriz A añadiéndole la columna formada por los términos independientes.

10.2 RESOLUCIÓN MATRICIAL DE UN SISTEMA

Un sistema de  m  ecuaciones lineales con  n  incógnitas puede resolverse matricialmente si la ecuación matricial A X = B tiene solución, para lo que debe existir A^-1. 

10.3 SISTEMAS EQUIVALENTES

Son los que tienen las mismas soluciones. Dado un sistema, debemos buscar otro equivalente de resolución más sencilla.

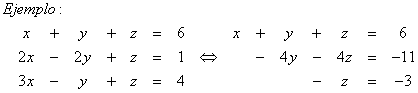
Para ello, podemos hacer con cualquiera de las ecuaciones E_i del sistema transformaciones del tipo E_i→ a E_i+b E_j con a≠0.

Es decir, está permitido:

1) Multiplicar o dividir los dos miembro de una ecuación por un número real distinto de cero.

2) Sumar o restar a una ecuación otra ecuación el mismo.

3) Sumar a una ecuación una combinación lineal de otra.

4) Suprimir una ecuación que sea combinación lineal de otra u otras.

5) Cambiar el orden de las ecuaciones y de las incógnitas.