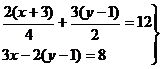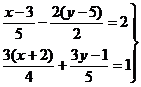Para resolver un sistema de ecuaciones lineales hemos estudiado varios métodos (sustitución, igualación y reducción). Ahora vamos a representar las ecuaciones ayudándonos de unas escenas y así completar los métodos de resolución de estos sistemas.
En el próximo tema vamos a estudiar el concepto de función o recta que en este temas utilizarás. Por ello no te preocupes si no entiendes como el programa genera la representación gráfica de las ecuaciones lineales.
a1 x + b1 y = c1 |
|
a2 x + b2 y = c2 |
1. Resuelve en tu cuaderno estos sistemas de ecuaciones lineales, aplicando alternativamente los métodos que conoces.
|
|
|
|
|
|
|
|
Comprueba los resultados que has obtenido con la escena, para ello sube o baja los valores de los coeficientes hasta obtener el mismo sistema.
En estos ejemplos la solución del sistema es única, es decir, hay un único valor para la variable x y para la variable y que satisface las dos ecuaciones. |
En temas anteriores has realizado operaciones con expresiones algebraicas, de modo que has conseguido llegar a una forma de expresión reducida. En este apartado se trata de realizar esa simplificación y posteriormente solucionar el sistema de ecuaciones lineales.
En la escena anterior necesitariamos calcular un sistema de ecuaciones equivalente que tuviera la forma general propuesta en el punto anterior, en cambio en esta sólo es necesario escribir teniendo en cuenta la posición de los paréntesis y que entre número y variable es necesario colocar el signo de multiplicación (*). No olvides dar "intro" una vez escrita para conseguir visualizarlo en la escena.
Observa en esta escena el siguiente ejemplo:
2. Resuelve en tu cuaderno estos sistemas de ecuaciones lineales. Recuerda primero obtener el sistema de ecuaciones lineales equivalente de la forma que te propusimos en el ejercicio 1 y posterioremente aplica alternativamente los métodos que conoces.
|
|
|
|
Comprueba los resultados que has obtenido con la escena.
Al igual que antes en estos ejemplos la solución del sistema es única, es decir, obtenemos un único valor para x y otro para y [lo llamaremos par (x,y)] que satisface las dos ecuaciones, lo que significa que las rectas asociadas tienen un sólo punto común. |
En posteriores temas clasificaremos los sistemas de ecuaciones lineales en función de las posibles soluciones que puedan tener. En este apartado observaremos ciertos sistemas de ecuaciones con resultados muy dispares. En ti, como buen investigador, está conseguir descubrir el porqué de estos resultados.
Observarás en esta escena que aparecen frases que determinan el tipo de ecuaciones, en este curso, como ya te comente anteriormente, no es interesante que lo interpretes, pero a modo de información te decimos que se llama a un sistema de ecuaciones compatible cuando tiene solución, si esta es única será determinado y sí no indeterminado. Para el caso que no tenga solución dicho sistema lo llamaremos sistema de ecuaciones incompatibles.
3. Resuelve en tu cuaderno estos sistemas de ecuaciones lineales. Observarás que en alguna hay algo extraño. Investiga que es lo que ocurre, para ello, posteriormente, ves a la escena y situa los valores y determina que es lo que pasa.
|
|
|
|
||
|
|
|
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
