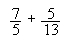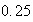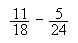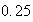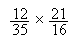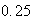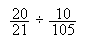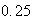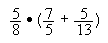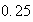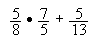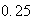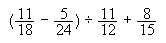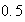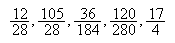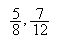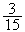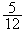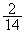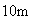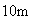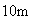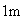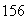-
Realitzeu les operacions següents donant-ne tots els detalls:
-
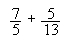
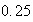 punts
punts
-
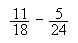
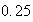 punts
punts
-
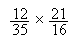
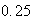 punts
punts
-
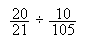
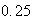 punts
punts
-
Realitzeu les operacions següents, tot indicant els passos que seguiu:
-
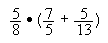
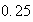 punts
punts
-
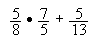
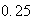 punts
punts
-
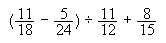
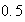 punts
punts
-
Donades les fraccions següents
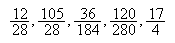
-
classifiqueu-les en classes d'equivalència.
-
doneu una fracció equivalent a cadascuna d'elles.
-
determineu la fracció irreductible representada per cadascuna d'elles.
-
Donades les fraccions
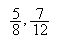
-
compareu-les numèricament,
-
representeu-les gràficament
(0.5 punts)
-
En Jorge, en Jordi i la Georgina estan empaperant el menjador de casa seva. De
moment, en Jorge n'ha empaperat
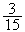 ,
en Jordi
,
en Jordi
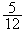 i la Georgina
i la Georgina
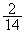 .
.
-
Qui ha treballat més fins ara? Qui ha treballat menys? Raona la teva
resposta.
-
Quina fracció del menjador han empaperat fins ara?
-
Quina fracció del menjador els queda per empaperar?
-
Els tres volen repartir la part que queda en tres parts iguals. Quines seran
aquestes parts?
(1 punt)
-
Donats els nombres naturals 120 i 96, calculeu-ne la descomposició
factorial en producte de potències de nombres primers. Utilitzant aquesta
descomposició, calculeu el màxim comú divisor i el mínim
comú múltiple dels dos nombres donats.
(1
punt)
-
Un contenidor de
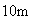 de llarg per
de llarg per
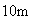 d'ample per
d'ample per
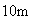 d'alt serveix per emmagatzemar caixes cúbiques de
d'alt serveix per emmagatzemar caixes cúbiques de
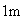 d'aresta que poden omplir el contenidor totalment. En aquest moment conté
d'aresta que poden omplir el contenidor totalment. En aquest moment conté
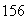 caixes.
caixes.
-
Quina és la fracció del contenidor que es troba plena ara mateix?
Quina es la fracció del contenidor que queda per omplir?
-
Aquesta tarda, han omplert una tercera part de l'espai que quedava. Quantes
caixes hi ha ara? Quantes caixes hi caben encara?
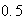 punts)
punts)
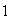 punt)
punt)
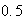 punts)
punts)
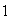 punts)
punts)
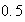 punts)
punts)