

-Actividades para realizar na clase.
- Actividades para realizar na casa.
Ámbito
Científico Tecnolóxico 4º E.S.O. Curso 2008-2009
I.E.S. Monte
Neme. Carballo. A Coruña
| Unidade
didáctica: Fraccións, decimais e porcentaxes Autora:
Ángela Núñez Castaín |
| Alumno/a: |
Nome: Data comezo:
Data finalización: |
Actividade 1: Representa
nos rectángulos que hai a continuación as fraccións:
![]()
| |
|
|
|
|
| |
||||
| |
|
|
|
|
Actividade
2.1: Coa axuda da primeira escena deste
epígrafe escribe dúas fraccións equivalentes a:
|
Actividade
2.2: Coa axuda da segunda escena deste epígrafe
escribe dúas fraccións equivalentes a:
|
Actividade
2.3: Coa axuda da segunda escena deste epígrafe,
relaciona na seguinte lista de fraccións as que son equivalentes:
![]()
| Fraccións
equivalentes |
Actividade 3.1. Reduce a común denominador as
fraccións:
a) 5/4 e 7/18
b) 7/3 e 8/27 c)
4/7 e 5/14 d) 3/100 e 5/4
| a) |
| b) |
| c) |
| d) |
Actividade 4.1: Compara
as seguintes parellas de fraccións reducindo a común
denominador. Despois comproba a solución na escena deste
epígrafe:
a) 3/2 e 4/3
b) 5/4 e 7/6
c) 19/5 e 23/6
| a) |
| b) |
| c) |
Actividade 5.1: No cubo de Rubik hai
8 cubiños de vértice que teñen 3 cores que representan 8/27 do
cubo, 12 cubiños de aresta con dúas cores que son 12/27 do cubo
¿Cantos cubiños hai no centro de cada cara e que teñen unha
soa cara de cor? ___![]()
¿Que fracción do total supoñen
estes cubiños? ___
¿Cantos cubiños hai que non teñen
ningunha cara de cor e non se ven? ___
¿Que fracción do total supoñen? ___
Comproba na primeira escea deste epígrafe
que a suma das catro fracción é 1. Fai o cálculo no seguinte
cadro:
| |
Actividade 5.2. Efectúa as seguintes sumas de
fraccións e compróbaas na segunda escena deste epígrafe:
a) 2/7 + 3/7
b) 2/3 + 5/7
c) 7/9 + 4/6
d) 7/6 + 9/6
| a) |
| b) |
| c) |
| d) |
Actividade 5.3. Efectúa as seguintes restas de
fraccións e compróbaas na segunda escena deste epígrafe:
a) 3/4 - 3/5
b) 3/5 - 4/5
c) 37/18 - 14/9
d) 37/9 - 18/9
| a) |
| b) |
| c) |
| d) |
Actividade 6:
Calcula a ) 1/5 de 100,
b) 3/4 de 200, c) 9/11 de
24200 e comproba na escena os resultados obtidos:
| a) |
| b) |
| c) |
Actividade 7: Efectúa as seguintes
multiplicacións e divisións de fraccións, simplificando o
máis posible os resultados, e comproba os resultados na escena:
a) 4/3 . 1/6
c) 2/5 . 3/8
e)20/9 . 15/4
b) 4/3 : 1/6
d) 2/5 : 3/8
f)20/9:15/4
| a) |
b) |
| c) |
d) |
| e) |
f) |
Actividade 8: Calcula
utilizando a escea a expresión decimal das fraccións:
a) 25/16, b) 15/24
e c) 25/27, compróbao coa calculadora e
compara os resultados:
| a) |
b) |
c) |
Actividade 9: Escribe dous
exemplos de números racionais que sexan: a) Números
enteiros, b) Números decimais exactos, c) Números
decimais periódicos puros, d) Números decimais periódicos
mixtos.
| a) |
b) |
c) |
d) |
Actividade 10.1.: Calcula a porcentaxe correspondente ás seguintes fraccións:
a) 1/2, b) 1/4, c) 3/4, d) 9/10, e) 1/5 f) 8/9
Comproba os resultados na escena.
| a) |
b) |
c)
|
| d) |
e) |
f) |
Actividade 10.2.: Expresa en forma de fracción as
seguintes porcentaxes:
a) 50%, b) 25%, c) 75%, d) 60%, e) 10%, f) 80%
Comproba os resultados na escena.
| a) |
b) |
c)
|
| d) |
e) |
f) |
Caso 1: Cálculo dun tanto por cento
dunha cantidade.
| Actividade
11.1.: Calcula o: a) 40% de 580.000 €, b)
80% de 500, c) 5% de 250, d) 10% de 2980, e) 20% de 5 millóns, f) 25% de 1 millón
Comproba os resultados na escena. |
||||||
| Actividade
11.2.: Calcula utilizando a fórmula: “parte por
cen dividido entre total” a porcentaxe que
representa: a) 6320 de 15800, b) 96 de 480,
c) 16 de 320,
d) 750 de 5000
Comproba os resultados na escena. |
||||||
Caso 2. Aumentos e diminucións
porcentuais.
Actividade 11.3.: Resolve os seguintes problemas e despois comproba os resultados na escena:
a) O número de parados, 184.300, que había nunha comunidade autónoma diminuíu un 19% ¿Cantos parados hai agora?
b) Nun pantano había 340 hl de auga. Diminuíu un 43% ¿Canta auga queda no pantano?
c) Este ano a gasolina subiu un 5%. Se a principios de ano custaba 0,799 €/litro, ¿canto costa agora o litro?
| a) |
| b) |
| c) |
Caso 3. Aumentos e diminucións
porcentuais encadeados.
| Actividade
11.4.: Resolve os seguintes problemas e despois
comproba os resultados na escena anterior: a)
A masa forestal dun bosque sufriu as seguintes
variacións ó longo de tres décadas: de 1950 a 1960
aumentou un 28%, de 1960 a 1970 diminuíu un 40%,de 1970
a 1980 aumentou un 15% ¿Que variación porcentual
experimentou de 1950 a 1980? b) Nun ano o prezo dun artigo sobe un 40%, despois baixa un 10% e, por último, baixa un 20% ¿Que variación porcentual experimentou ó longo do ano?
|
||||||||||||||||||||||||||||||||||||
Caso
4. Cálculo da cantidade inicial, coñecendo a variación
porcentual e a cantidade final.
|
||||||||||||||||||||||||||||||||||||
Actividades para realizar na casa
a)
![]() b)
b) ![]()
a)
![]() =
=
b)
![]() =
=
b)
![]() =
=
b) ![]() =
=
c)
![]() =
=
d)
![]() =
=
b) -![]()
a)
![]() =
=
b)
![]() =
=
a)
![]() =
=
b)
![]() =
=
c)
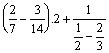 =
=
d)
![]() =
=
e)
![]() =
=
f)
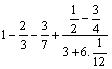 =
=
a)
![]() =
=
b)
![]() =
=
c)
![]() =
=
d)
![]() =
=
e)
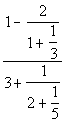 =
=
| Actividades
do libro de texto: Resolver nesta páxina e nas dúas
seguintes os exercicios: 8, 9, 10, 11, 12 (páxina 15);
33 (páxina 22) |
|
| |
|
| |
|
| Fai
un resume dos contidos tratados nesta unidade: |
|
| Comenta
a túa impresión sobre este xeito de “facer
matemáticas” |
|
Rematei este caderno o día ___ de
__________ de 2008
Asdo.: ______________________