
TEOREMA DEL COSENO
Para resolver el resto de los tipos de problemas necesitamos otro teorema, el del coseno.Que dice que: en un triángulo cualquiera se cumple que
a2=b2+c2-2bccosA
Es decir que un lado cualquiera al cuadraddo es igual a la
suma de los cuadrados de los otros dos lados menos el doble del producto de estos dos
lados por el coseno del ángulo que forman.(Este teorema es la generalización del teorema
de Pitagoras para triángulos no rectángulos, si A=90º, cos90º=0, se obtiene el teorema
de Pitagoras).
Mueve los vértices del triángulo y observa como se sigue cumpliendo la fórmula del teorema. Comprueba con tu calculadora que esto es cierto para el triángulo que tiene A=40º, B=75º y C=65º
Si quieres ver la demostración del teorema pulsa aquí
Con esto ya podemos resolver los problemas de los tipos que nos faltaban:
3. Resolución de un triángulo del que se conocen dos lados y el ángulo comprendido entre ellos.Si de un triángulo conocemos A=40º, b=7 cm. y c=10 cm. Calcular el resto de los elementos. Observa en la escena los datos que tienes y los que te faltan.
Intenta resolverlo en tu cuaderno y comprueba las soluciones pulsando aquí .
Modificar en la escena los valores de A, B y c, para ver el planteamiento de los posibles problemas, que encntrarás en EJERCICIOS
4. Resolución de triángulos en los que conocemos
los tres lados. Si de un triángulo conocemos a=10 m, b=15 m. y c=20 m..
Calcular el resto de los elementos del triángulo. Puedes ver la solución aquí
Modificar en la escena los valores de A, B y c, para ver el planteamiento de los posibles problemas, que encontrarás en EJERCICIOS
Autor: José Ángel López Mateos.
I.E.S.Dámaso Alonso
DEMOSTRACIÓN DEL TEOREMA DEL COSENO
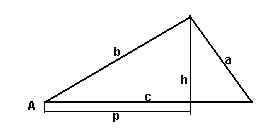
Observa que el triángulo ha quedado dividido en dos
triángulos rectángulos.Por el teorema de Pitagoras se tiene que a2=(c-p)2+h2
y h2=b2-p2 . Luego se obtiene a2=(c-p)2+h2=(c-p)2+b2-p2=c2+p2-2pc+b2-p2=c2+b2-2pc
y como p=bcosA tenemos el teorema
Volver
3.Aplicando el teorema del coseno:
a2=72+102-2x7x10xcos40º=49+100-140x0.766=149-107.2462=41.7537
luego a=6.4617 cm.
Aplicando de nuevo el teorema del coseno 72=(6.4617)2+102-2x10x6.4617xcosB, luego cosB=0.7177196, y B=44.1334º y entonces el C=95.8665º.
72=(6.4617)2+102-2x10x6.4617xcosB, luego cosB=0.7177196, luego B=44.1334º y entonces el C=95.8665º
4.También aquí aplicamos el teorema del coseno:
102=202+152-2x20x15xcosA, despejando cosA=0.875, y A será el arco cuyo coseno es 0.875 A=28.95º.
Aplicando de nuevo el teorema del coseno (aunque también se puede aplicar el del seno) 202=102+152-2x10x15xcosC, cosC=-0.25 y C=104.47
Sólo falta B=180-A-C=46.5724º