Paradoja de la dicotomía
Se supone comúnmente que un atleta puede desplazarse desde el punto de salida (A) hasta la meta (B). Sin embargo, según Zenón, esto es imposible. Su argumento es el siguiente: antes de llegar a la meta el atleta deberá recorrer la mitad de la distancia y alcanzar el punto medio de A y B, esto es, I1. Alcanzado el punto I1, antes de llegar a B deberá recorrer la mitad de la distancia que le queda y alcanzar el punto medio de I1 y B, esto es, I2. Continuando el argumento indefinidamente, el corredor deberá, antes de llegar a B, recorrer infinitos trayectos en un tiempo finito, lo cual es imposible.
En este argumento Zenón asume que el espacio es continuo y, por tanto, infinitamente divisible. Sin embargo, no hace lo mismo con el tiempo, lo que da lugar a la paradoja. Veamos primero qué es lo que hace con el espacio:
Suposición: el espacio es infinitamente divisible
Aunque pueda resultar sorprendente en un principio, es posible sumar infinitas cantidades y que el resultado sea finito. Un ejemplo sencillo es el de las progresiones geométricas, que son aquellas sucesiones en las que cada término se obtiene multiplicando al anterior por una cantidad constante llamada razón. Si dicha razón es menor que uno es fácil demostrar que la suma de los infinitos términos de la progresión se obtiene mediante la fórmula S = a1/(1 - r), donde a1 es el primero de los términos.
Un caso especialmente intuitivo es el de la progresión 1/2, 1/4, 1/8, 1/16, 1/32... Parece claro que si primero cogemos la mitad de la unidad, y luego la mitad de lo que queda, y luego la mitad de lo que queda, y así "hasta el infinito", acabaremos cogiendo la unidad completa:
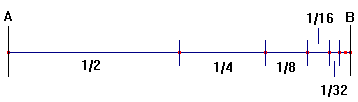
Efectivamente: aplicando la fórmula anterior para la suma, se tiene:
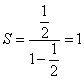 .
.
El caso planteado por Zenón es esencialmente el mismo: supongamos que la distancia a recorrer es L. Entonces los intervalos a recorrer por el atleta serán L/2, L/4, L/8..., cantidades que resultan ser los términos de una progresión geométrica de razón 1/2 cuya suma es:
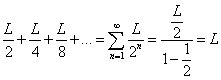
Es decir, que no hay problema en subdividir el espacio infinitamente.
¿Y el tiempo?
Si la velocidad del atleta es v (que consideramos constante por comodidad), el tiempo que tardará en recorrer el primer intervalo será L/2v, y el segundo L/4v, y así sucesivamente. Zenón en este punto dice que el corredor nunca podrá llegar a la meta porque recorrer los infinitos intervalos le llevaría un tiempo infinito. Pero se equivoca: si sumamos todos los tiempos, tenemos:
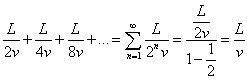
que es una cantidad de tiempo finita.
Conclusión
A no ser que alguna razón nos lo impida, si aceptamos la continuidad del espacio debemos aceptar la del tiempo, lo cual nos autoriza a recorrer infinitos intervalos espaciales en un tiempo finito.
Conviene indicar que los cálculos anteriores no demuestran que el movimiento sea posible, sino que el argumento de Zenón no es correcto.
Una variante
Antes de llegar al punto medio de A y B, esto es, I1, el corredor debería llegar al punto medio de A e I1, esto es, I2. Y antes de llegar a I2 debería de llegar al punto medio de A e I2, esto es, I3. Repitiendo el proceso indefinidamente sumimos al corredor en una extraña inmovilidad, pues antes de alcanzar cualquier punto de la trayectoria debe haber pasado por una cantidad infinita de ellos.