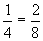F R A C C I O N E S E Q U I V A L E N T E S |
||
|---|---|---|
|
Imagínate que tienes dos tartas: una de chocolate y otra de nata. Supongamos que sean dos tartas iguales pero que estén divididas de distinta manera. Si una tarta está dividida en menos trozos, los trozos serán más grandes y si está dividida en más trozos, los trozos serán más pequeños. Para comerte la misma cantidad de tarta de cada una, debes coger más trozos de aquella que esté más dividida.
En el primer caso, la tarta está dividida en 4 trozos y en el segundo caso en ocho. Es evidente que los trozos de la primera tarta son más grandes que los de la segunda y que, para comerte la misma cantidad de las dos tartas debes coger un trozo de la primera y dos de la segunda. Pero ambas fracciones representan la misma cantidad, por tanto decimos que las dos fracciones son equivalentes, es decir, iguales.
|
||
|
||
|
||
|
||
|
||