

Auxiliares
Auxiliares.
Se llaman auxiliares a las constantes, variables, vectores (listas de variables), funciones y algoritmos que el autor o la autora de una escena de Descartes puede definir y utilizar. Los auxiliares de una escena pueden editarse usando el panel de configuración de auxiliares, al que se accede seleccionando "Auxiliares" en la ventana de edición.
El Panel de configuración de Auxiliares tiene este aspecto.
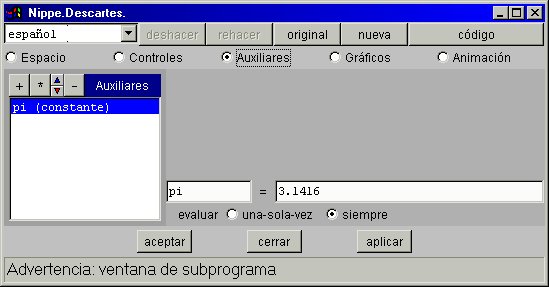
Como ocurre en otros paneles se distinguen dos partes el cuadro de edición a la izquierda y el de configuración a la derecha, en el cuadro de edición aparece la lista de todos los auxiliares de la escena (en el ejemplo sólo aparece la constante pi). El cuadro de configuración es diferente para cada tipo de auxiliar, en él se pueden editar todos los parámetros que definen al auxiliar seleccionado en la lista. Más adelante se muestran y explican los diversos paneles.
Nota: Si se hace un clic sobre la etiqueta azul de Auxiliares, aparecerá una ventana con un área de texto que contiene el código de todos los auxiliares, uno en cada línea. Este texto se puede editar manualmente y pulsando aceptar se actualiza el editor con los cambios realizados. Las y los desarrolladores experimentados pueden encontrar este método de edición muy cómodo y útil para cierto tipo de modificaciones.
Para crear un auxiliar nuevo hay que pulsar el botón + que se encuentra arriba a la izquierda de la lista. Al pulsarlo aparece una ventana de diálogo con un selector y un campo de texto. El selector sirve para elegir el tipo de auxiliar que se desea definir. Las opciones son: variable, constante, vector, función y algoritmo (ver la figura).
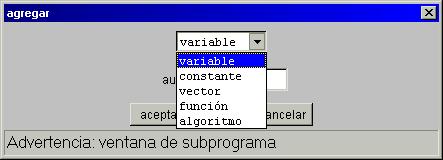
Una vez elegido el tipo de auxiliar deseado el usuario debe escribir en el campo de texto el nombre del auxiliar que servirá de referencia para usarse en otros auxiliares, en los gráficos o en la animación. El programa ofrece al autor un nombre por defecto que consta de una letra: v (variable), c (constante), V (vector), f (función) o a (algoritmo) según el tipo del auxiliar, seguida de un número que corresponde a la posición del nuevo auxiliares en la lista. Se recomienda al autor no utilizar los nombres por defecto sino asignar nombres adecuados al contenido de la escena. El ejemplo siguiente corresponde a una nueva variable a la que se le ha dado el nombre ángulo.
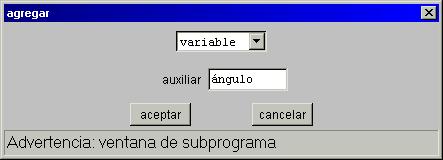
El resto de esta página se dedica a explicar en detalle el funcionamiento y los paneles de configuración de cada tipo de auxiliar.
1. Variables.
Las variables son los auxiliares más flexibles. Su valor puede ser cualquier expresión definida en términos de los parámetros de los controles, de otros auxiliares que aparezcan antes en la lista o de x e y.
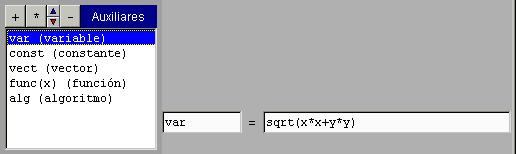
Las variables se evalúan cada vez que se utilizan, esto es lo que los hace tan útiles. Por ejemplo, si se define una variable como R=raíz(x^2+y^2) y se define una gráfica de tipo ecuación con la expresión R=2, entonces se obtiene la gráfica de la circunferencia de radio 2. En otras palabras, las variables pueden utilizarse como abreviaturas de expresiones más o menos complejas.
Las variables también pueden utilizarse como constantes pero no es recomendable hacerlo porque ello puede ralentizar el funcionamiento de la escena. En principio las variables deben utilizarse únicamente cuando dependen de x o y. En cualquier otro caso es preferible utilizar constantes (de las que se evalúan siempre).
2. Constantes.
Las constantes son los auxiliares utilizados con mayor frecuencia. El valor de una constante puede definirse como una expresión cualquiera en términos de los identificadores de los controles y de otras constantes que aparezcan antes en la lista, pero no en términos de x e y.
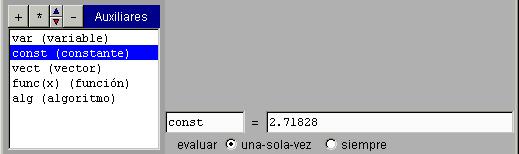
Hay dos tipo de constantes:
1) las que se evalúan "una sola vez", que podrían llamarse constantes absolutas, y
2) las que se evalúan "siempre", es decir, cada vez que se toca un pulsador, se mueve un control gráfico o se va a dar un nuevo paso en la animación.
Las constantes que se evalúan siempre y las variables que no dependen de x o y son muy semejantes en apariencia, y de hecho pueden utilizarse en las mismas circunstancias, pero en tales casos siempre es preferible utilizar constantes. La razón es que las constantes que se evalúan siempre en realidad se evalúan solamente cuando hay un cambio en la escena, en cambio las variables, si aparecen en la definición de un gráfico, se tienen que evaluar muchas veces en cada cambio de la escena, lo cual pueden llegar a ralentizar la respuesta del programa.
3. Vectores.
Un vector es una lista de constantes. Un vector tiene un identificador y un tamaño, que es su longitud o número de elementos. El ejemplo de la figura siguiente corresponde a un vector con identificador vect y de tamaño 3. Los tres elementos del vector tienen valor 0.
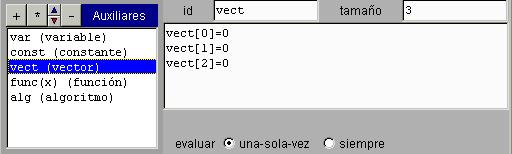
La manera de hacer referencia a un elemento de un vector es escribir el identificador del vector seguido del número del elemento entre corchetes. Los elementos de un vector se numeran siempre comenzando por 0.
El área de texto que aparece en el panel de configuración de un vector sirve para asignar valores a (o inicializar ) los elementos del vector. No es necesario utilizar el área de texto, también se puede utilizar un algoritmo para inicializar un vector. En particular cuando un vector tiene muchos elementos (por ejemplo 1000), la manera correcta de inicializar sus elementos es utilizar un algoritmo.
Por defecto los vectores se evalúan una sola vez, es decir, son constantes absolutas, pero si el autor desea que dependan de los parámetros de una escena, deberá elegir evaluar "siempre".
4. Algoritmos.
Los algoritmos constituyen un sistema sencillo para inicializar vectores y para programar procesos de cálculo más o menos complejos.
La figura muestra el panel de configuración de un algoritmo.
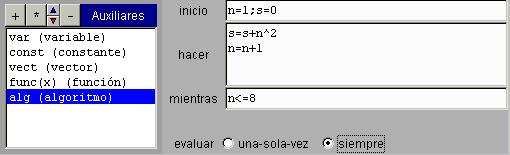
El panel tiene un campo de texto etiquetado como inicio, un área de texto etiquetada como hacer y otro campo de texto etiquetado como mientras.
El el campo inicio se puede escribir una serie de asignaciones y llamadas a otros algoritmos separadas por ; . En el área de texto hacer se puede escribir también una serie de asignaciones y llamadas a otros algoritmos pero separadas por ; o por un salto de línea. Para llamar a un algoritmo en el inicio o hacer de otro, basta escribir su nombre (como si fuera una asignación) y separarlo por ; en inicio o por un salto de línea en hacer. En el campo mientras se puede escribir una expresión booleana.
Un algoritmo funciona así: primero realiza las asignaciones y llamadas a otros algoritmos que se indican en inicio; luego realiza las asignaciones y llamadas a otros algoritmos indicadas en hacer y luego verifica si se cumple la condición contenida en mientras. Si la condición mientras se cumple entonces vuelve a ejecutar hacer y vuelve a verificar la condición mientras. El proceso continúa hasta que la condición mientras deja de cumplirse o se han llegado a 10000 repeticiones (este límite es una válvula de seguridad para proteger al autor y al usuario de posibles errores que pudieran bloquear el navegador). Si la condición mientras se deja en blanco el algoritmo realiza las asignaciones en hacer una sola vez.
La estructura de los algoritmos de Descartes es en realidad un bucle de programación que corresponde al do .. while de los lenguajes C y Java y al repeat ... while de Pascal .
Para realizar una asignación condicional se puede utilizar la construcción: A?a:b donde A es una expresión booleana y a y b son los dos valores que se asignarán según se cumpla o no la condición A. Por ejemplo y=(x>0)?sen(2*pi*x):0 asigna a y el valor sen(2*pi*x) si x>0 y asigna 0 si x<=0. Esta construcción corresponde (parcialmente) al if ... else ... de los lenguajes de programación.
La combinación de bucles inicio - hacer - mientras , las asignaciones condicionales A?a:b y la posibilidad de llamar algoritmos desde otros algoritmos ofrece muchas posibilidades para la programación de procesos de cálculo relativamente complejos.
El panel de algoritmos permite decidir si éstos se evalúan una sola vez o siempre. Los algoritmos pueden servir para inicializar vectores. Los que se evalúan una sola vez se ejecutan sólo al iniciarse la escena y cuando se pulsa el botón inicio, así que sirven para inicializar vectores que permanecen constantes durante toda la interacción del usuario con la escena. Los algoritmos que se evalúan siempre, se ejecutan cada vez que hay un cambio en un control, ya sea numérico o gráfico, con lo cual sirven para evaluar vectores que dependen de los parámetros de los controles. Cuando un algoritmo se llama desde otro, se ejecuta, independientemente de si está marcado como evaluar una sola vez o siempre.
La estructura de bucles inicio - hacer - mientras de los algoritmos se utiliza también en las funciones algorítmicas y en la animación. De hecho la animación es un algoritmo especial que refresca la escena después de cada paso por hacer.
5. Funciones.
Las funciones asignan un número real a cada valor de su variable (o a cada conjunto de valores de sus variables). Las funciones tienen un identificador (o nombre), una o más variables (que no son más que una lista de identificadores) y una expresión en términos de esas variables. Pueden usarse todas las funciones matemáticas habituales.
Estos son ejemplos de funciones de una variable con sus identificadores y sus variables:
expresión |
identificador |
variable |
| f(x)=sen(3*x+2) | f | x |
| g(y)=A*exp(-(y^2)/(s^2)) | g | y |
| Area(radio)=(pi*radio^2)/2 | Area | radio |
Estos son ejemplos de funciones de dos o más variables con sus identificadores y sus variables:
expresión |
identificador |
variables |
| f(x,y)=raíz(x^2+y^2) | f | x,y |
| Fun(x,y,z) | Fun | x,y,z |
| Volumen(a,b,c)=4*pi*a*b*c/3 | Volumen | a,b,c |
Los nombres específicos de las variables de una función no son importantes, sólo sirven para identificar las variables dentro de la expresión y asignarles allí un papel.
Las funciones se evalúan solamente cuando son llamadas explícitamente (por ejemplo por un algoritmo, por un gráfico, por la animación o por la constricción de un control gráfico que se mueve).
El panel de configuración de una función tiene este aspecto:
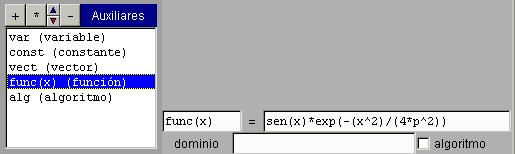
El campo donde aparece el identificador de la función debe incluir los identificadores de las variables entre paréntesis y separados por comas para dar sentido a la expresión que aparece al lado derecho. La expresión que aparece a la derecha del signo = puede ser o incluir un término condicional, por ejemplo
func(x)=(x<0)?0:1.
es la función que vale 0 para x<0 y 1 para x>=0. Una expresión booleana vale 1 cuando es verdadera y 0 cuando es falsa por lo cual la función anterior también podría escribirse como
func(x)=(x>=0),
o bien usando la función indicadora ind, también se podría escribir como:
func(x)=ind(x>=0),
Al final de esta página se ofrece una lista de todas las funciones matemáticas y los operadores que reconoce el analizador de expresiones de Descartes, aparte de las que se definen explícitamente en cada escena. Estas funciones y operadores pueden usarse en cualquier sitio donde Descartes espera una expresión, incluyendo el campo de texto de un control numérico.
El dominio puede ser una expresión booleana en términos de las variables de la función. El programa utiliza el dominio para decidir si intenta evaluar la función. Si en un punto la expresión del dominio no se cumple, la evaluación no se intenta y el programa genera una excepción, con lo cual, si por ejemplo se está dibujando la gráfica de esta función, el dibujo que corresponde a este punto no se realiza y se pasa al siguiente punto. Cuando el campo del domino está vacío se considera que el dominio de la función no tiene restricciones, es decir, cualquier conjunto de valores de sus variables está en el dominio.
Cuando el programa intenta evaluar una función en un punto donde tiene una singularidad, se genera una interrupción, igual que si el punto no estuviera en el dominio. Por lo tanto no es necesario excluir del dominio de una función sus puntos singulares, el programa ya lo hace automáticamente. Sólo hay que especificar el dominio si se desea restringir el dominio natural de una función.
A veces no se puede definir una función solamente mediante una expresión, sino que su evaluación requiere un proceso más complicado. En estos casos el autor puede marcar algoritmo, con lo cual aparece arriba del campo para la expresión de la función, el panel de definición de un algoritmo, y en él puede describir el algoritmo de evaluación de la función. El siguiente ejemplo muestra cómo puede una función utilizar un algoritmo. Se trata de una función Fact(x) que calcula el factorial del mayor entero menor o igual que x.

El algoritmo que se define en este panel se ejecuta cada vez que se quiere evaluar la función, por lo cual los valores calculados en el algoritmo pueden utilizarse para definir el valor de la función.
Las funciones pueden tener cualquier número de variables, incluso cero. Para evaluar una función sin variables se debe escribir un par de paréntesis después de su nombre (por ejemplo func()). Las funciones sin variables pueden servir como algoritmos de cálculo que devuelven un valor real. También puede haber funciones que no devuelven ningún valor, las cuales pueden usarse como algoritmos que admiten parámetros. En el ejemplo siguiente se presenta una función de siete variables Euler(x,y,vx,vy,ax,ay,dt) llamada Euler que es en realidad una implementación del método de integración de Euler para calcular la posición de una partícula que parte de la posición (x,y) con una velocidad (vx,vy) y que se mueve con aceleración constante (ax,ay) durante un tiempo dt y mientras y>0.
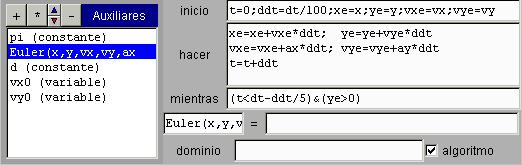
Esta función puede llamarse desde cualquier otra función, desde un algoritmo o desde la animación. y al llamarla no hay que asignarla a una variable, basta escribir su nombre y los parámetros que se le pasan separados por comas.
6. Funciones matemáticas y operadores.
Las funciones matemáticas que reconoce el analizador de expresiones de Descartes, aparte de las que esté explícitamente definidas en una escena, son las siguientes:
Funciones de una variable (x):
sqr sqr(x)=x*x
sqrt sqrt(x)=raíz cuadrada de x
raíz sqrt(x)=raíz cuadrada de x
exp exp(x)=exponencial natural de x=e^x
log log(x)=logaritmo natural de x
log10 log10(x)=logaritmo base 10 de x
abs abs(x)=valor absoluto de x
ent ent(x)=mayor entero n tal que n<x
sgn sgn(x)=signo de x (1 si x>0,-1 si x<0,0 si x=0)
ind ind(b)=indicadora de b (1 si b=true, 0 si b=false)
sin sin(x)=seno de x
sen sen(x)=seno de x
cos cos(x)=coseno de x
tan tan(x)=tangente de x
cot cot(x)=cotangente de x
sec sec(x)=secante de x
csc csc(x)=cosecante de x
sinh sinh(x)=seno hiperbólico de x=(exp(x)-exp(-x))/2
senh senh(x)=seno hiperbólico de x=(exp(x)-exp(-x))/2
cosh cosh(x)=coseno hiperbólico de x=(exp(x)+exp(-x))/2
tanh tanh(x)=tangente hiperbólica de x=sinh(x)/cosh(x)
coth cot(x)=cotangente hiperbólica de x=cosh(x)/sinh(x)
sech sech(x)=secante hiperbólica de x=1/cosh(x)
csch csch(x)=cosecante hiperbólica de x=1/senh(x)
asin asin(x)=ángulo cuyo seno es x
asen asen(x)=ángulo cuyo seno es x
acos acos(x)=ángulo cuyo coseno es x
atan atan(x)=ángulo cuyo coseno es x
Funciones de dos variable (x,y):
min minx,y)=mínimo de x e y
max max(x,y)=máximo de x e y
También hay un número aleatorio con distribución uniforme en el intervalo [0,1]:
rnd
Los operadores y otros símbolos que el analizador de expresiones reconoce son:
( paréntesis izquierdo
) paréntesis derecho
= igualdad, operador binario que da un resultado booleano.
# desigualdad, operador binario que da un resultado booleano
| operador binario de disyunción equivalente a OR ( O )
& operador binario de conjunción equivalente a AND ( y )
> mayor que, operador binario que da un resultado booleano
< menor que, operador binario que da un resultado booleano
+ signo mas, operador binario de suma
- signo menos: binario de resta o unario de cambio de signo
* por, operador binario de multiplicación
/ entre, operador binario de división
^ operador binario de exponenciación (a^b=ab )
% módulo, operador binaro, resto de una división entera
~ operador unario booleano de negación.
? pregunta, sólo para asignaciones condicionales (P)?a:b
: separador, sólo para asignaciones condicionales (P)?a:b
| José
Luis Abreu León Revisado para Descartes Web 2.0 por José R. Galo Sánchez |
||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2009 | ||