Descartes VECTORES: DEFINICIÓN E COORDENADAS 
Xeometría Analítica
 
1. mAGNITUDES ESCALARES E VECTORIAIS
Unha magnitude dícese que é ESCALAR cando basta con dar un número e a correspondente unidade para que quede determinada.
Unha magnitude dícese que é VECTORIAL cando necesitamos máis información para que quede determinada.
Esta unidad interactiva requiere la máquina virtual de Java J2RE.

1.1- Nesta escena indica cales magnitudes son escalares e cales vectoriais; anota as razóns no teu caderno.




2. vECTORES: COMPOÑENTES E COORDENADAS.
Un VECTOR é un segmento orientado que se determina por dous puntos A e B, e a orde destes.
O primeiro punto chámase orixe e o segundo extremo, e escríbese .

Ten os seguintes elementos:
  • Módulo: é a lonxitude do segmento AB
  • Dirección: é a recta sobre a que está situado o vector ou calquera outra paralela
  • Sentido: é a forma de percorrer o segmento AB, é dicir de fixar a orixe e o extremo.
Podemos escribir un vector con dous números (x, y), as súas coordenadas, que nos dan unha idea de como é o movemento que se fai ao pasar da orixe o seu extremo:
  • a súa primeira coordenada, x,  indícanos cantas unidades movémonos en horizontal; se é positiva o movemento é hacia a dereita e se é negativa hacia a esquerda.
  • a súa segunda coordenada, y,  indícanos cantas unidades movémonos en vertical; se é positiva o movemento é hacia arriba e se é negativa hacia abaixo.


Esta unidad interactiva requiere la máquina virtual de Java J2RE.

2.1 Nesta escena observas as coordenadas da orixe e do extremo do vector, e ademáis as coordenadas do vector. 
Move a orixe e o extremo e observa que pasa. Qué relación hai entre as coordenadas dos puntos e as do vector?

2.2 Utilizando a o resultado anterior, calcula as coordenadas dos seguintes vectores, de orixe A e extremo B:
  • A (-1, 2)      B(2, 0)
  • A (2, 0)       B(-1, 2)
  • A (2, 3)       B(4, 7)
  • A (-2, 3)      B(-4, 7)
  • A (0, 0)       B(6, 2)
  • A (-2, 1)      B(-5, 1)
Comproba na escena que os teus cálculos son correctos

2.3 Cantos vectores se poden formar cos puntos A (1, 2), B(3, 5) e C(4, 4)? Calcula as súas cooordenadas e represéntaos no teu caderno.

2.4 Cantos vectores se poden formar cos puntos A (4, 1), B(2, 5)  C(0, 3) e D(-1, -2)? Calcula as súas cooordenadas e represéntaos no teu caderno.

2.5 Calcula as coordenadas do punto A se o vector  ten de coordenadas (-1, 3) e B(5, 2).

2.6 Calcula as coordenadas do punto B se o vector  ten de coordenadas (2, 4) e A(-2, -6).
Esta unidad interactiva requiere la máquina virtual de Java J2RE. 2.7 Imos calcular o módulo dun vector aplicando o teorema de Pitágoras. Fai tí o cálculo no teu caderno e logo comproba se é correcto.
  • A(1, 1)     B(2, 3)
  • A(-4, 1)    B(5,-2)
  • A(3,-2)     B(1,-1)
  • A(-3, 0)    B(0, 4)
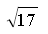2.8 Con orixe no punto (2, 4) debuxa e escribe as coordenadas dun vector de módulo ; existe máis dun vector? razoa a resposta.

2.9 Con extremo no punto (0, 0) debuxa e escribe as coordenadas dun vector de módulo 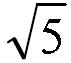;existe máis dun vector? razoa a resposta.


       
           
  Autora: Mª Isabel Hermida Rodríguez
 
Ministerio de Educación, Cultura y Deporte, Política Social y Deporte. Ano 2010
 
 

Licencia de Creative Commons
Os contidos desta unidade didáctica están baixo unha licenza de Creative Commons se non se indica o contrario.