CÓNICAS

3. LA HIPÉRBOLA

I. LA HIPÉRBOLA

Una hipérbola es una curva abierta de dos ramas, producida por la intersección de un cono circular recto y un plano que corta  las dos secciones del cono.

La fórmula matemática de la hipérbola, centrada en el origen de coordenadas es

 

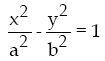
   Los puntos de corte de la hipérbola y el eje OX (abscisas) son:

A(a, 0) y A´(-a, 0)

   El eje real es el segmento AA´. El semieje real es a.

   No hay puntos de corte de la hipérbola y el eje OY (ordenadas).

   El eje imaginario es el segmento BB´. El semieje maginario es b.

   Los puntos F(c, 0) y F´(-c, 0) se llaman focos.

   Para hallar los focos necesitamos conocer un nuevo valor c llamado semidistancia focal, que verifica la siguiente ecuación: c2= a2 + b2.

    Se llama excentricidad al cociente entre c y a.

1. Cambia a y b para ver cómo calcular los vértices y los focos de la hipérbola

2. Dibuja la hipérbola anterior en tu cuaderno, con todos los elementos que observas.

3. Calcula todos los elementos anteriores si a=4 y b=2. Comprueba que coincide con los valores que se obtienen en la escena anterior.

II. DEFINICIÓN MATEMÁTICA DE HIPÉRBOLA

Definición. Una hipérbola es el lugar geométrico de los puntos cuya diferencia de distancias a dos puntos fijos llamados focos es constante.

4. Cambia los valores de a y b para ver cómo cambia la hipérbola.

5. Mueve el punto P y comprueba la definición de hipérbola. Comprueba que efectivamente la diferencia de distancias de P a los focos F y F´ es constante.

6. Copia la definición de hipérbola en tu cuaderno.

III. ASÍNTOTAS DE LA HIPÉRBOLA

Existen dos rectas simétricas (asíntotas de la hipérbola) que pasan por el centro geométrico de la misma y de forma que la hipérbola no las toca, aunque la distancia entra la curva y las asíntotas es cada vez menor sin llegar a cortarse nunca.

7. Observa cómo se dibujan las asíntotas de la hipérbola y copia en tu cuaderno:

8. Cambia los valores de a y b e intenta averiguar las ecuaciones de las dos asíntotas. Comprueba que has realizado bien los cálculos de las asíntotas mirando la escena.

IV. TRAZADO DE LA HIPÉRBOLA

En este apartado vamos cómo se puede dibujar una hipérbola sin ninguna de las definiciones anteriores. De forma muy visual podremos ir cambiando el número de pasos e intuir la gráfica de la hipérbola.

  1. Dibujamos una circunferencia de centro O y radio a (en rojo).
  2. Tomamos en su exterior un punto cualquiera F’(-c, 0) (en azul, que será uno de los focos)
  3. Unimos el punto anterior F’ con un punto P de la circunferencia mediante una recta (en rojo).
  4. Sobre el punto P trazamos la perpendicular a la recta anterior (en azul).
  5. Repetimos los pasos 3 y 4 tantas veces como sea posible.

  NOTA: Si tomamos el valor de a mayor que el valor de c, veremos que se dibuja una elipse.

   

9. Cambia los valores del radio a de la circunferencia y del número de pasos p. Observa cómo se va "dibujando" la hipérbola.

10. Copia en tu cuaderno los pasos que debes dar para trazar una hipérbola por este método e intenta realizar en tu cuaderno el dibujo de una hipérbola.

Volver al inicio

 

 
  Fco. Javier Payán Jiménez
 
Ministerio de Educación, Cultura y Deporte. Año 2005
 
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.