
 |
TRIGONOMETRICAL RATIOS OF ACUTE ANGLES |
| Geometry | |
| 1. TRIGONOMETRICAL RATIOS IN A RIGHT-ANGLED TRIANGLE | ||
|
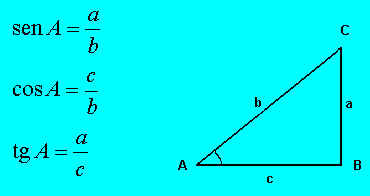
The trigonometrical ratios of an acute angle are defined by using the sides of the triangle. However, they do not depend on the length of these sides. The sine, cosine and tangent ratios of the acute angle in a right-angled triangle, as illustrated in the diagram, where B=90º, b is the hypotenuse and a and c are the other two sides can be defined using the following formulae: If we increase the length of the sides of the triangle and draw lines parallel to side a we produce triangles which are similar to the original one. Therefore, the trigonometrical ratios of angle A are the same as they only depend on the size of the angle (in degrees or in radians). We are going to use the Descartes program to prove that the formulae are true. |
 |
|
| 1.- Change
the length of b until it is equal to 12.
2.- Note that the trigonometrical ratios do not change when the angle is 30º, as illustrated in the diagram. Change angle A to 45º and 60º. 3.- Work out the trigonometrical ratios of the following angles: 15º, 1 radian, 85º and 0.3 radians.
4.-Try and construct a right-angled triangle whose sides measure 3,4 and 5. Work out the size of angle A. |
||
| 2. A ONE-UNIT HYPOTENUSE TRIANGLE | ||
|
Since the values of the trigonometrical ratios in a right-angled triangle do not depend on the length of the sides, you can work with a triangle whose hypotenuse is equal to one unit, i.e. b = 1. This will simplify the calculations considerably. The side opposite the angle is equal to the sine and the side adjacent to the angle is equal to the cosine. |
||
| 5.-
Work
out the trigonometrical ratios of the following angles: 15º, 45º,
60º, 1 radian, 85º and 0.3 radians.
6.- Can you see a connection between the three trigonometrical ratios? Try and write a formula to show this connection.
7.- Work out the value for angle A when : sin A=0.5, cos A=0.75 and tan A =2.75 |
||
| Miguel García Reyes | ||
 |
||
| Spanish Ministry of Education. Year 2001 | ||
![]()
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.