

TEOREMAS DE PAPPUS, DESARGUES Y PASCAL
Basándose en los teoremas de Menelao y Ceva es posible demostrar algunos de los teoremas más importantes de la geometría plana.
Uno de ellos es el teorema de Pappus, demostrado por primera vez por Pappus de Alejandría alrededor del año 300 a.C. Su papel en los fundamentos de la Geometría Proyectiva no fue reconocido hasta casi dieciséis siglos después.
Se llama figura de n vértices a una figura formada por n puntos diferentes del plano que están numerados 1,2,...n y n rectas que unen los puntos 1-2, 2-3, ..., (n-1)-n.
Dichos puntos se llaman vértices de la figura y las rectas se llaman lados.
Si llamamos A,B,C,D,E,F a los vértices de una figura de 6 lados, los vértices A-D, B-E, C-F se llaman opuestos.
Los lados opuestos son AB y DE, BC y EF, CD y FA.
Teorema de Pappus:
Si una figura de seis vértices tiene sus vértices situados consecutivamente en dos rectas, entonces los puntos de intersección de sus lados opuestos están alineados.
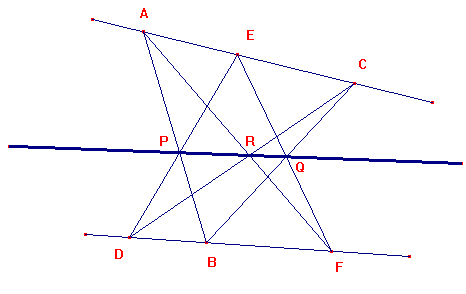
1.- Experimenta moviendo los vértices de la figura y comprueba la veracidad del teorema.
2.- Comprueba que para que el teorema se verifique son intrascendentes las medidas de longitudes o ángulos (lo que pone de manifiesto su naturaleza "proyectiva"). Tampoco importa el orden de los puntos (no importa cuál es el que se sitúe entre los otros dos).
3.- Demuestra que si A,B,C son tres puntos de una recta, B,D,F de otra y si las rectas AB y CD son paralelas a DE y FA respectivamente, entonces EF es paralela a BC.
Definiciones:
Dos triángulos ABC y A'B'C' se dice que son copolares si AA', BB' y CC' son concurrentes.
Se dice que son coaxiales si los puntos de intersección de BC y B'C', CA y C'A', AB y A'B' están alineados.
El teorema de Desargues para dos triángulos parece que fue publicado por Girard Desargues (1.591-1.661) en una obra de perspectiva en 1.636, tres años antes de que se publicara su Brouillon Project. Este teorema se ha hecho básico en la Geometría Proyectiva.
El geómetra francés Jean-Victor Poncelet (1.788-1.867) hizo del teorema de Desargues el fundamento de su teoría de figuras homológicas.
Teorema de Desargues:
Dos triángulos copolares son coaxiales, y viceversa.
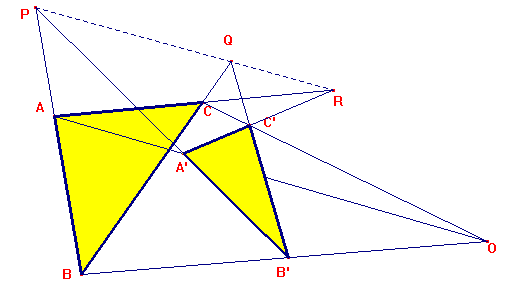
1.- Experimenta moviendo los vértices de ambos triángulos y comprueba la veracidad del teorema.
2.- Experimenta y comprueba su "naturaleza proyectiva" (son intrascendentes las medidas de longitudes o de ángulos).
Inspirándose en la obra de Desargues, Blaise Pascal (1.623-1.662) obtuvo su teorema del hexagrama místico para una cónica general cuando sólo tenía 16 años. Nadie sabe cómo lo demostró el propio Pascal, ya que su demostración original se ha perdido. Sin embargo, antes de perderse, la demostración fue conocida y alabada por Leibniz .Las consecuencias de este teorema son muy numerosas y atractivas, y se ha hecho una cantidad casi increíble de investigación sobre su configuración.
Teorema del "hexagrama místico" o hexágono de Pascal (para una circunferencia):
Los puntos de intersección de los tres pares de lados opuestos de un hexágono (convexo o no) inscrito en una circunferencia, están en una recta (llamada recta de Pascal del hexágono).
El teorema también es cierto para una cónica general.
1.- Mueve los vértices del hexágono sobre la circunferencia y comprueba la veracidad del teorema.
2.- ¿Qué ocurre si el hexágono es regular? Interpreta el resultado.
3.- Experimenta para el caso de que el hexágono no sea convexo.
|
|||||||||||||||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.