| 1. ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA. |
Una ecuación de primer grado es una igualdad algebraica que se expresa de la forma a x + b = 0 ; donde a y b son números reales cualesquiera y a es distinta de cero. La solución será única y vendrá dada por x = -b/a. |
Resolver una ecuación de primer grado con paréntesis consiste en eliminar los paréntesis aplicando las reglas de la suma y de la multiplicación para conseguir llegar a una expresión similar a la dada en la definición y así conseguir obtener la solución de la misma. |
|
|
En la siguiente escena te proponemos que repases el método de resolución de ecuaciones de primer grado para la ecuación:
4(2x + 3 - x) - 6 (x-1) = 9 (x+1)
Para ello resuelvelo en tu cuaderno de trabajo y posteriormente aumenta el número de pasos para comprobar que lo has realizado correctamente.
1. Resuelve en tu cuaderno, según el método estudiado las siguiente ecuaciones que posteriormente utilizarás:
- 3(2x+5-x) - 4(x+9-2x) = 4x - 3(x+5)
- 2(x-3+2x) + 8(x-7-5x) = 2(x-1) - 3(4x-2)
- 4(x+2) - 3(x-1) = x + 11
- -2(x+18-3x+2) - 4 = 7x - 2(4x-3)
- -4(2x+8-5x) - 4 (x-2) = -3
En el caso de que sólo exista solución, esta es única, es decir, hay un único valor para la variable x que satisface la ecuación. No debes confundir el término de ecuación con el término de identidad. |
|
| |
|
En la siguiente escena vamos a ver la representación gráfica de las ecuaciones de primer grado. Para ello, simplifica las ecuaciones hasta que sea del tipo ax + b = 0 y observa donde se encuentra el resultado. Observa el ejemplo del punto anterior que esta resuelto en la escena: 4 (2x + 3 - x) - 6 (x-1) = 9 (x+1) 2. Busca en tu cuaderno de trabajo las expresiones obtenidas anteriomente del tipo ax + b = 0 e introduce los valores de a y b en la escena para poder comprobrar que los resultados obtenidos en las ecuaciones del ejercicio anterior son las correctas.
- 3(2x+5-x) - 4(x+9-2x) = 4x - 3(x+5)
- 2(x-3+2x) + 8(x-7-5x) = 2(x-1) - 3(4x-2)
- 4(x+2) - 3(x-1) = x + 11
- -2(x+18-3x+2) - 4 = 7x - 2(4x-3)
- -4(2x+8-5x) - 4 (x-2) = -3
3. ¿Cómo resuelve la escena las ecuaciones de primer grado? |
| |
|
En esta última escena vamos a ver obtener la solución de las ecuaciones de primer grado, introduciendo directamente la ecuación.
Para ello, debes introducir todos los símbolos de las operaciones incluidos los signos de producto, que es un asterisco.
Observa el ejemplo del punto anterior que esta resuelto en la escena:
4 (2x + 3 - x) - 6 (x-1) = 9 (x+1)
4. Introduce las siguientes ecuaciones y comprueba que los resultados obtenidos coinciden con los obtenidos en las ecuaciones de los ejercicios anteriores.
- 3(2x+5-x) - 4(x+9-2x) = 4x - 3(x+5)
- 2(x-3+2x) + 8(x-7-5x) = 2(x-1) - 3(4x-2)
- 4(x+2) - 3(x-1) = x + 11
- -2(x+18-3x+2) - 4 = 7x - 2(4x-3)
- -4(2x+8-5x) - 4 (x-2) = -3
|
Resolver una ecuación de primer grado con denominadores consiste en aplicar el m.c.m. y obtener las fracciones algebraicas equivalentes para poder aplicar la regla de la suma y la multiplicación para conseguir llegar a una expresión similar a la dada en la definición. |
|
Resuelve las ecuaciones propuesta en tu cuaderno de trabajo. Posteriormente introduce en la escena la ecuación propuesta para comprobar si has conseguido el mismo resultado.
Para ello, debes introducir todos los símbolos de las operaciones incluidos los signos de producto, que es un asterisco, y el de la división.
Observa el ejemplo en la escena:
(2x + 3) / 2 = (x+1) / 4
5. Haz las siguientes ecuaciones en tu cuaderno. Introduce las ecuaciones en la escena y comprueba que los resultados obtenidos coinciden con los obtenidos en tu cuadeno.
- 3(2x+5)/2 - 4(x+9)/6 = 4x/3
- 2(x-3)/3 + 8(x-7-5x)/9 = 2(x-1)/4
|
|
| 2. ECUACIONES DE SEGUNDO GRADO. |
Una ecuación de segundo grado es una igualdad algebraica que se expresa de la forma a x^2 + b x + c = 0 ; donde a, b y c son números reales cualesquiera y a es distinta de cero.
|
Resolver una ecuación de segundo grado consiste en aplicar la siguiente fórmula
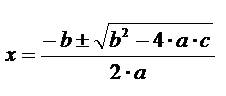
La expresión
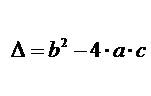
se denomina determinante y nos dice cuantas soluciones podemos obtener.
|
En la siguiente escena te proponemos dos ecuaciones, una de ellas, la de segundo grado se controla con los controles inferiores a, b y c, mientras que la otra, la de primer grado, determinará su representación gráfica introduciendo el valor de "y", pulsa enter para confirmar el valor. Utilizarás en función del ejercicio una o las dos ecuaciones. |
|
|
6. Resuelve en tu cuaderno las siguientes ecuaciones
- 2 x^2 - 10 x + 12 = 0
- 5 x^2 + 5 x - 30 = 0
- 5 - 4 x - x^2 = 0
Comprueba en la escena, manipulando los controles a, b y c, lleva el punto para conocer la solución y comprobarlo con los resultados que has obtenido en tu cuaderno.
7. ¿Qué conclusión sacas cuando se representan las ecuaciones de segundo grado si está igualada a cero? ¿Sería distinto si lo igualas a otro valor?
8. Comprueba tu teoría en las siguientes ecuaciones, que previamente has solucionado en tu cuaderno.
- 2 x^2 - 10 x + 12 = 4
- x^2 + x - 6 = 6
- 5 - 4 x - x^2 = 5
Ahora utiliza la recta que puedes editar.
|