
SISTEMAS DE ECUACIONES
Resolución algebraica y gráfica
Dado un sistema de ecuaciones de la forma : 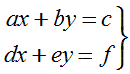 con a, b, c, d, e y f números reales.
con a, b, c, d, e y f números reales.
Método de Sustitución: Realizaremos los siguientes pasos:
1º.- Aislamos una de las dos incógnitas de una de las dos ecuaciones.
2º.- Sustituimos
el valor obtenido en la ecuación del sistema que aún no
hemos utilizado, quedando así una ecuación de primer
grado que tenemos que resolver.
3º.- Sustituimos el valor obtenido en el segundo paso en la
expresión obtenida en el primero y obtendremos el valor de la
incógnita que faltaba.
Los valores obtenidos x e y forman la solución del sistema.
| NOTA: a, b, c,
d, e y f comprendidos entre -100 y 100 (
Con otros valores no podremos
realizar la resolución con el applet, pero si se puede
resolver
manualmente.) |
1.-
Realiza en tu cuaderno los siguientes sistemas de ecuaciones lineales
por el método de sustitución y luego comprueba las
soluciones obtenidas con el applet.
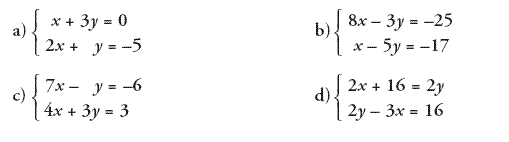
Método de Igualación: Realizaremos los siguientes pasos:
1º.- Aislamos una de las dos incógnitas de las dos ecuaciones.
2º.- Igualamos
los valores obtenidos, quedando así una ecuación de primer grado que tenemos que
resolver.
3º.- Sustituimos el valor obtenido en el segundo paso en
la expresión obtenida en el primero y obtendremos el valor de la
incógnita que faltaba.
Los valores obtenidos x e y forman la solución del sistema.
2.-
Realiza en tu cuaderno los siguientes sistemas de ecuaciones lineales
por el método de igualación y luego comprueba las soluciones obtenidas
con el applet.
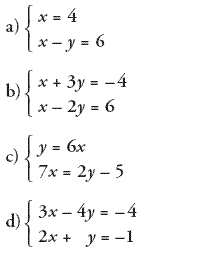
Método de Reducción: Realizaremos los siguientes pasos:
1º.-
Multiplicamos cada ecuación por el valor absoluto del
coeficiente que tiene la x en la otra ecuación . Tendremos que
tener en
cuenta el signo que queda en los coeficientes de x de las dos
ecuaciones, de ser el mismo cambiaremos todos los signos de una de
las ecuaciones. Después sumaremos las ecuaciones y resolveremos
la ecuación de primer grado que obtendremos.
2º.- Repetiremos el mismo proceso con la y.
Los valores obtenidos x e y forman la solución del sistema.
3.-
Realiza en tu cuaderno los siguientes sistemas de ecuaciones lineales
por el método de reducción y luego comprueba las soluciones obtenidas
con el applet.

Método Gráfico:
Representaremos en unos ejes de coordenadas las rectas determinadas por
cada una de las ecuaciones del sistema. El punto donde se cortan ambas
rectas (x,y) es la solución del sistema.
4.- Comprueba cada uno de los sistemas que has resuelto en tu cuaderno con el applet del método gráfico.
5.-
Resuelve en tu cuaderno los siguientes sistemas por sustitución,
igualación y reducción. ¿Que sucede? Introduce
estos sistemas en el applet del método gràfico y explica
que sucede en cada caso.
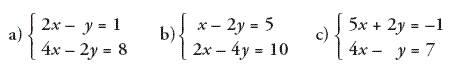 .
.
| |
Àngels Folch Mateu |
 |
|
|
Ministerio de Educación, Cultura y Deporte. Año 2009 |
| |
|

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.

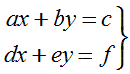 con a, b, c, d, e y f números reales.
con a, b, c, d, e y f números reales.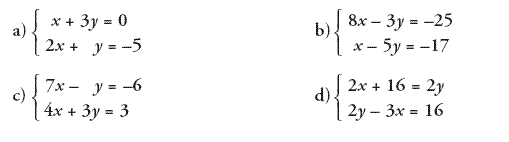
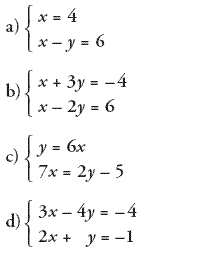

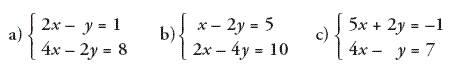 .
.![]()