
OPERACIONES CON FRACCIONES (Repaso)
Un poco de historia.
Las
fracciones y el ser humano han estado ligados desde la antigüedad, pero al no poseer
buenos sistemas de numeración recibieron durante mucho tiempo notaciones poco
claras e inadecuadas para las aplicaciones prácticas.
Se
cree que las fracciones surgieron en el Antiguo Egipto, al tener que repartir
panes entre personas pero cuando había más personas que panes. Los egipcios
sólo utilizaban fracciones unitarias (cuyo denominador es 1) y una a la que
daban un simbolismo especial, la fracción ![]() .
.
Los
babilonios fueron los primeros en utilizar una notación racional expresando los
números de forma parecida a la actual.
La
expresión de una fracción poniendo el numerador arriba y el denominador abajo
se la debemos a los hindúes, pero ellos no ponían entre ambos la raya
horizontal que ponemos en la actualidad, esa raya se la debemos a los árabes.
Definición de fracción
Las
fracciones, en su significado más simple, nos indican el número de partes que
tomamos de un “todo” al que llamamos unidad. Al número de partes que tomamos lo
llamamos numerador (que colocaremos encima de la raya de fracción) y al número
de partes iguales en que dividimos la unidad, denominador (el
cual se colocará bajo la raya de fracción).
Para escribir una fracción con las letras del abecedario debemos observar su denominador: si el denominador es menor o igual que 10, la fracción se lee diciendo el numerador y luego el ordinal del denominador (tres quintos). Si el denominador es mayor que 10 se lee diciendo el numerador y luego el número del denominador seguido del sufijo avo/s (nueve catorceavos).
Fracciones equivalentes. Comparación de
fracciones.
Se dice que dos fracciones son equivalentes si representan la misma parte de la unidad.
Con
la ayuda de la siguiente escena observa si son equivalentes las fracciones que
se proponen en el ejercicio siguiente. (Resuelve
los ejercicios que se propongan en tu cuaderno de trabajo ayudándote de las
escenas).
1.- Comprueba si son equivalentes las
fracciones:
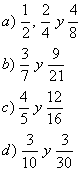
Como
habrás observado y recordarás, para construir una fracción equivalente a otra
dada podemos emplear dos procedimientos: el primero consiste en multiplicar el
numerador y el denominador por un mismo número natural (proceso que recibe el
nombre de amplificación); y el segundo consiste en dividir tanto el numerador
como el denominador por un mismo número (siempre y cuando sea posible) ,
proceso al que llamamos simplificación.
Con
la ayuda de la escena anterior resuelve en tu cuaderno de trabajo el siguiente
ejercicio.
2.- a) Construye tres fracciones equivalentes a
una de tu elección mediante el proceso de amplificación.
b) Construye dos fracciones equivalentes a
la fracción ![]() mediante simplificación.
mediante simplificación.
Comparación de fracciones
Recuerda
que para comparar dos o más fracciones lo más recomendable es que construyas
fracciones equivalentes a las dadas, pero que tengan el mismo denominador. Para
ello, se suelen amplificar ambas empleando el mínimo común múltiplo.
Con
la ayuda de la escena anterior trata de responder al siguiente ejercicio en tu
cuaderno de trabajo.
3.- ¿Qué fracción es mayor?
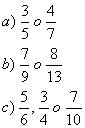
Operaciones con fracciones.
Suma/
resta de fracciones
Recuerda
que para sumar o restar dos o más fracciones hemos de tener el mismo denominador
(el cual se obtiene haciendo el mínimo común múltiplo de los denominadores).
Una vez obtenido, se trasforman las fracciones en otras equivalentes cuyo
denominador sea el obtenido y, finalmente, se suman los nuevos numeradores.
Con
la ayuda de la siguiente escena, realiza las operaciones de suma y resta, en tu
cuaderno de trabajo, que se proponen a continuación. (Si has de simplificar el resultado ayúdate de la escena
anterior).
4- Resuelve:
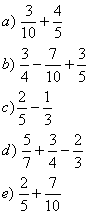
Multiplicación
y división de fracciones.
Para
multiplicar fracciones has de recordar que lo único que hay que emplear es el
producto de números naturales. Para multiplicar dos fracciones se multiplicaban
los numeradores para obtener el nuevo numerador y los denominadores, por otro lado,
para obtener el nuevo denominador.
Ejemplo:
![]()
Para
dividir dos fracciones se utiliza también el producto de números naturales,
pero esta vez se realiza haciendo productos cruzados, es decir, para hallar el
numerador nuevo se multiplica el numerador de la primera fracción por el
denominador de la segunda; y para calcular el nuevo denominador se multiplica
el denominador de la primera por el numerador de la segunda.
Ejemplo:
![]()
5.- Utiliza la escena anterior para realizar las operaciones que se
proponen a continuación. No olvides realizarlas en tu cuaderno de trabajo. Si necesitas simplificar, ayúdate de la escena segunda.
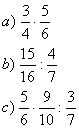
6.- Escribe en tu cuaderno de trabajo algunas
operaciones combinadas con fracciones y resuélvelas ayudándote de las escenas
necesarias de la práctica.
|

