EL CONJUNTO DE LOS NÚMEROS REALES
Análisis
 
1. NÚMEROS REALES
El conjunto de números reales está formado por los números racionales y los irracionales y se puede representar en una recta en la que se determinan un origen y  una unidad, de modo que a cada número real le corresponde un único punto de la recta, y a cada punto de la recta se le asigna un único número real.

La noción de orden en el conjunto de los números reales permite definir en la recta real los siguientes conjuntos numéricos:
  • Intervalo abierto de extremos a y b. Es el conjunto de número reales, cuyos elementos son mayores que a y menores que b: .
  • Intervalo cerrado de extremos a y b. Es el conjunto de número reales, cuyos elementos son mayores o iguales que a y menores o iguales que b: .
  • Intervalo semiabierto o semicerrado de extremos a y b. Observa en este caso, que solo está incluido uno de los extremos:

Esta unidad interactiva requiere la máquina virtual de Java J2RE.
Pulsando el botón inicio te aparece un nuevo intervalo  finito. Con el control conjuntos numéricos puedes cambiar de intervalo. Si mueves el punto de color blanco, puedes ver los puntos que pertenecen a ese intervalo.

Con los controles a y b puedes mover los extremos de cada uno de los intervalos.

1.- En un intervalo cerrado, comprueba que contiene los extremos.

2.- En un intervalo abierto, comprueba que no contiene los extremos.

3.- En un intervalo sermiabierto o semicerrado, comprueba que solo contiene a uno de los extremos.

A parte los intevalos de extremos finitos descritos anterioremente, tenemos los intervalos en los que alguno de los extremos es infinito. Dichos intervalos son los  conjuntos numéricos , que se representan mediante semirectas en la recta real.
  • :  es el conjunto numérico de todos los números reales x que son mayores que a, sin incluir a.
  • : es el conjunto numérico de todos los números reales x que son mayores o iguales que a, incluido a.
  • : es el conjunto numérico de todos los números reales x que son menores que a, sin incluir a.
  • : es el conjunto numérico de todos los números reales x que son menores  o iguales que a, incluido a.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.
Pulsando el botón inicio te aparece un nuevo intervalo  infinito. Con el control intervalo infinito puedes cambiar de intervalo. Si mueves el punto de color blanco, puedes ver los puntos que pertenecen a ese intervalo.

Con el control a puedes mover el extremo de cada uno de los intervalos.

4.- En un intervalo infinito cerrado por la izquierda o por la derecha, comprueba que contiene al extremo a.

5.- En un intervalo infinito abierto por la izquierda o por la derecha, comprueba que no contiene al extremo a.

6.- Escribe en tu cuaderno el intervalo que te aparece y el conjunto de números reales que representa la semirecta.

2. VALOR ABSOLUTO
Se define el valor absoluto de un número a, |a|, como el mayor de los dos números -a y a: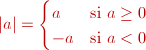

Propiedades:









Esta unidad interactiva requiere la máquina virtual de Java J2RE.
Pulsando el botón inicio te aparece una nueva función de valor absoluto. Con los controles a y b puedes cambiar también la función.

1.- ¿En qué le afecta a la función si cambiamos el valor del parámetro a?

2.- ¿Y si modificamos el parámetro b?

Mueve el punto P de color blanco, por la gráfica de la función. Fíjate en el valor que toma la función en dicho punto.

3.- Comprueba que se cumplen las tres primeras propiedades del valor absoluto que hemos definido anteriormente.
4.- Resuelve en tu cuaderno las siguientes ecuaciones: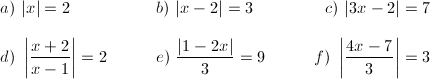


5.- Resuelve en tu cuaderno las siguientes desigualdades. Representa las soluciones en forma de intervalo.
 
3. ENTORNO ABIERTO DE CENTRO a Y RADIO r>0
Definimos un entorno abierto de centro el punto a y radio r>0, al conjunto de números reales comprendidos entre a-r y a+r:


Por la definición de valor absoluto, la desigualdad |x| < r, es equivalente a la desigualdad . Por ello, tenemos que:


Utilizando el concepto de valor absoluto de un número, podemos reescribir la definición de entorno abierto como:


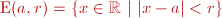Esta unidad interactiva requiere la máquina virtual de Java J2RE.
Pulsando el botón inicio te aparece un nuevo entorno abierto centrado en el punto a y de radio r. Con el control radio puedes cambiar el radio del entorno. Si mueves el punto de color blanco, puedes ver los puntos que pertenecen a dicho entorno abierto.

1.-Escribe en tu cuaderno el entorno abierto de centro a y radio r que te aparece y el conjunto de números reales que representa dicho entorno abierto.

2.-¿Qué representa geométricamente |x-a|?
   
   
           
  Mª del Carmen Torres Alonso
 
© Ministerio de Educación. Año 2011
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.

f