
UNIDAD DIDACTICA
PROGRAMACIÓN LINEAL
Estudio gráfico y analítico de los semiplanos que origina una recta en el plano
Consideremos la recta y=x. Esta recta divide al plano en dos
semiplanos. Haremos desplazar un punto P por todo el plano cartesiano y
observaremos las inecuaciones de los semiplanos, según de la
pertenencia del punto P a ellos.
1.- Desplazar el punto P por el plano, y aparecerán coloreados cada
semiplano que origina la recta y=x, así como sus respectivas
inecuaciones.
2.- Observar que si el punto P pertenece a la recta y=x, entonces P no
pertenece a ninguno de los semiplanos (no aparecen lógicamente
coloreados).
Regiones
del plano (gráfica y analíticamente) que verifican la resolución de un
sistema de dos inecuaciones de primer grado con dos incógnitas
Consideremos las bisectrices del primer y segundo cuadrantes, es decir,
las rectas y = x e y = -x. Vamos a ver las cuatro regiones donde se
verifican todas las posibilidades de combinar las inecuaciones
correspondientes. Desplazaremos, de nuevo un punto P por el plano y en
cada región aparecerán las inecuaciones que verifica P.
3.-
Desplazar el punto P por el plano, y aparecerán escritas las
inecuaciones que verifica la región del plano (coloreada) donde se
encuentra P.
Problema
de programación lineal donde se calculan los valores máximo y mínimo de
una función en una región factible cerrada y acotada
Enunciado del problema:
Una empresa fabrica dos tipos de televisores A y B,
a un coste por televisor de 200 y 100 euros respectivamente. Sabemos
que el número de televisores del tipo A, fabricados diariamente, no
supera en 4 unidades los del tipo B. Y que entre ambos no se superan
diariamente los 30 televisores fabricados. También se sabe que el
proceso productivo no permite fabricar diariamente menos de dos
televisores del tipo A, ni menos de 5 del tipo B. Se pide:
a) Formular el sistema de inecuaciones asociado al enunciado.
b) Dibuja la región factible y calcula sus vértices.
c) Calcula cuántos televisores del tipo A y del tipo B, maximizan y cuántos minimizan el coste de producción diaria.
4.- Con el pulsador k haz
desplazar la recta que contiene al vector (función objetivo) y te irán
apareciendo los vértices de la región factible (coloreada en azul
turquesa), así como el nombre que se le ha dado a cada uno de ellos con
sus coordenadas, especificando los que cumplen la condición de
maximizar ó minimizar la función.
5.- Para ver lo explicado en el apartado anterior, también lo puedes
hacer, pulsando en el PLAY de la animación y la recta se desplaza sola. Para que la recta vuelva a la posición inicial, darle a la tecla de rebobinar para atrás (3ª tecla).
Problema de programación lineal donde la región factible no está acotada pero existe mínimo para la función objetivo z
Enunciado del problema:
En una granja de pollos se da una
dieta "para engordar" con una composición mínima de 15 unidades de una
sustancia A y otra de 15 de una sustancia B. En el mercado sólo se
encuentran dos clases de compuestos: el tipo X con una composición de
una unidad de A y cinco de B, y el tipo Y, con una composición de cinco
unidades de A y una de B. El precio del tipo X es de 10 euros, y el del
tipo Y también 10 euros. Se pregunta:
¿Qué cantidades se han de comprar de cada tipo para cubrir las necesidades con un coste mínimo?
6.- Con el pulsador k se puede desplazar paralelamente al vector z (función objetivo), y al pasar por los vértices de la región factible aparecen los puntos con sus respectivas coordenadas y se señala aquél donde z alcanza el mínimo valor.
7.- Observar, realizando ZOOM varias veces que la región factible (coloreada en naranja) es no acotada, no existiría el máximo de z.
Problema
de programación lineal donde el máximo de z se alcanza en un punto
(matemáticamente) pero por la naturaleza del problema la solución
máxima la verifican 3 puntos
Enunciado del problema:
Un quiosco vende bolígrafos a 20 céntimos de euro y cuadernos a 30
céntimos de euro. Llevamos 1,20 euros y pretendemos comprar los mismos
cuadernos que bolígrafos por lo menos.
¿Cuál será el número máximo de piezas que podemos comprar?
8.- Pulsar en k para desplazar la recta que contiene al vector z paralelamente a él. Obsérvense los vértices de la región factible (coloreada en amarillo).
9.- Comprobar al desplazar paralelamentela la recta que contiene a z, que la solución matemática sería el punto B, pero por la naturaleza del problema
(al tener que ser los bolígrafos y los cuadernos, números naturales,
pues no podemos comprar medio boligrafo, ni un cuarto de cuaderno) la solución del problema planteado serían los puntos C, D y E.
10.- Como consecuencia de la actividad anterior, deducir que la región factible es la coloreada en amarillo (punto de vista matemático), pero que la región factible para el problema sólo contiene un número finito de puntos.
Ejercicio de programación lineal cuya solución (mínimo, en este caso) se alcanza en un número infinito de puntos (segmento)
Enunciado del ejercicio:
Considerar la función z=1.5x + y y el conjunto de restricciones:
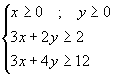
Comprobar que esta función alcanza su valor mínimo en mas de un punto.
11.- Mediante el pulsador de k, la recta que contiene al vector z, se desplaza en paralelo a él por la región factible (coloreada en violeta). Se van obtenieno los vértices, y se observa que el lado AD del polígono que representa la región factible es solución del problema, siendo, además, todos los infinitos puntos del segmento AD la solución mínima del ejercicio.
12.- A medida que desplazamos
la recta citada en la anterior actividad, aparecen las coordenadas de
los puntos, y en un rectángulo (sombreado de verde claro) el segmento
que minimiza a z).
| |
Emiliano
Perdiguero García
|
 |
|
|
Ministerio de Educación, Cultura y Deporte. Año 2010 |
| |
|

