3.
Una inecuación lineal con dos incógnitas es cualquier desigualdad que, directamente o mediante transformaciones de equivalencia, se pueden expresar de una de las formas siguientes:
ax+by+c > 0; ax+by+c < 0; ax+by+c £ 0 ó ax+by+c ³ 0con a, b y c reales y a¹0, b¹0
La solución general está formada por el conjunto de todos los pares (s1,s2) que verifican la inecuación.
Gráficamente, la solución, son los puntos del plano que tienen por coordenadas (s1,s2).
Para resolver esta inecuación recurrimos a la ecuación
ax+by+c=0 , que es la ecuación de una recta y que, para cada uno de sus puntos, tiene por ordenada.
La inecuación anterior, mediante transformaciones de equivalencia, se puede expresar, dependiendo del signo de relación, como
, es decir, la verifican todos los puntos que tiene una ordenada(y) menor (o mayor o igual, según el signo de relación) que la ordenada de los puntos de la recta.
Por lo tanto, la solución general de una inecuación lineal con dos incógnitas es un semiplano, del que la recta anterior es su frontera.
EJEMPLO, resuelve
x-3y-3 < 0
- situamos en el plano la recta de ecuación
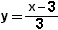
- el semiplano solución viene dado por los puntos cuya ordenada es
. Es decir, los puntos del semiplano cuya ordenada es mayor, que la ordenada de la recta.
ax+by+c.
En esta escena vemos la representación gráfica de las soluciones de la inecuacion:
x-3y-3 < 01.-Mueve el punto P(x,y) para saber si cumple o no cumple la inecuación.
2.- Modifica los parámetros a, b y c y vuelve a responder a la primera cuestión.
¿Cuántas soluciones tiene la inecuación?
Las soluciones forman un semiplano, que será abierto(la recta frontera no pertenece a la solución) o cerrado(la recta frontera forma parte de la solución) dependiendo de si es una desigualdad estricta o no, respectivamente.
EJERCICIO:
Resuelve en tu cuaderno de trabajo las inecuacones:
a) 3x+4y > 12; b) 2x+3y £ 6; c) x + 2y + 4 ³ 0
Para cada una de las inecuaciones anteriores, cambia en la escena los valores de a, b y c y el signo de relación y comprueba los resultados que has obtenido.
SISTEMAS
Un sistema de inecuaciones lineales con dos incógnitas es un conjunto de dos o más de estas inecuaciones.
El par (s1,s2) es solución del sistema si satisface simultáneamente todas las inecuaciones.
A la región solución, si existe, se le llama también región factible. Si es vacía, el sistema es incompatible.
La resolución de un sistema de inecuaciones se realiza encontrando la región del plano intersección de los semiplanos que son solución de cada una de las inecuaciones que forman el sistema:
- Consideremos el sistema formado por dos inecuaciones lineales con dos incógnitas. Representamos, en el plano cartesiano, los semiplanos solución de ambas inecuaciones.
- Las soluciones del sistema son las coordenadas de los puntos que pertenecen a la vez a los dos semiplanos solución.
Veamos, en la siguiente escena, la resolución gráfica de un sistema de inecuaciones lineales con dos incógnitas.
Para hacer el estudio gráfico, expresamos el sistema en la forma; transformando, si es necesario, las inecuaciones iniciales.
(el signo de la desigualdad será el que se nos dé en las inecuaciones que nos propongan):
Consideremos, en la escena, el sistema formado por las dos inecuaciones lineales con dos incógnitas:
2x+2y+3 <0
-x+y+3 <0
Aparecen representada en la figura los semiplanos solución de ambas inecuaciones(en naranja y azul, respectivamente).
Las soluciones, (s1,s2), del sistema son las coordenadas de los puntos que pertenecen a la vez a los dos semiplanos solución.
La solución es la región intersección de los semiplanos, región factible(en verde)
EJERCICIO:
Resuelve en tu cuaderno de trabajo los sistemas de inecuacones:
a); b)
; c)
Para cada una de las inecuaciones anteriores, cambia en la escena los valores de a, b, c, d, e, y f y los signos de las relaciones y comprueba los resultados que has obtenido.
Diego González Álvarez
Ministerio de Educación, Cultura y Deporte. Año 2005