Los
sistemas de inecuaciones de primer grado con dos incógnitas son
los que
pueden ponerse en la forma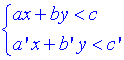 
(*), siendo a, b, c, a', b' y c'
números
reales.
(*) Puede ser
cualquier otra desigualdad: >, £
ó
³.
Para resolver
un sistema como este, resolveremos cada una de las
inecuaciones por separado y luego escogeremos las soluciones
comunes de ambas. Veamos los siguientes ejemplos:
|
Ejemplo
8.1.-
Resuelve el sistema de inecuaciones siguiente:
|
|
En
la escena hemos representado las rectas y=-2x-3 e y=2x+1.
Si
movemos el punto P
por el plano, irá dejando un rastro
amarillo
en el semiplano formado por todos aquellos puntos que son
solución de la 1ª inecuación y si hacemos lo propio con Q, éste irá
dejando un rastro
azul en el semiplano formado por los
puntos que son solución de la 2ª inecuación. En consecuencia, las
soluciones del sistema (región factible) son los puntos del
plano que hay en la parte donde hay rastros con los dos
colores.
|
|
En
nuestro caso, la región factible es la marcada
con el número IV (incluidos los puntos
correspondientes de las dos rectas pues en las dos
inecuaciones aparece el =).
|
|
|
