LA RELACIÓN DE SEMEJANZA
EN EL PLANO. HOMOTECIA.
Figuras semejantes.
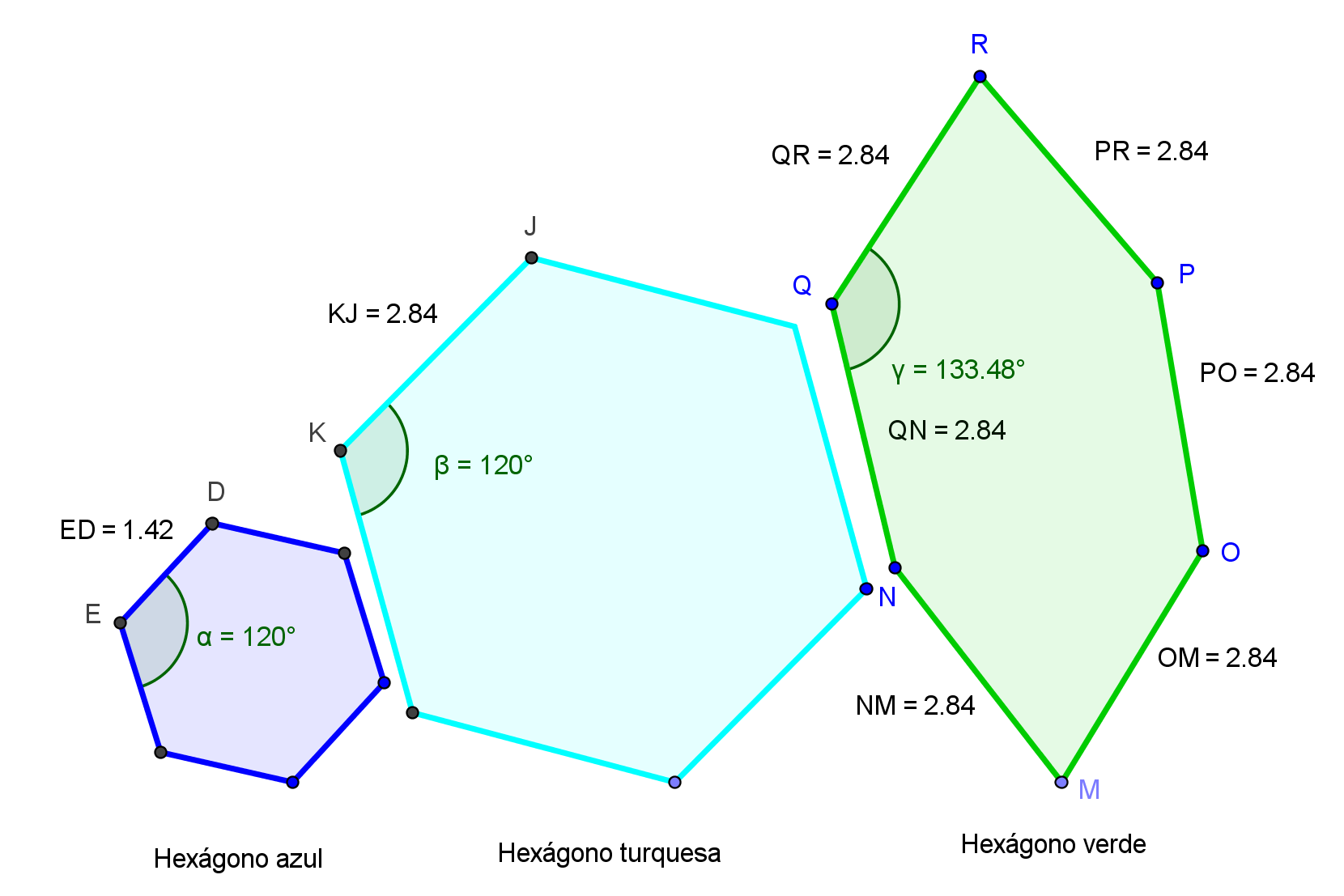
Empezaremos observando tres hexágonos:
| Si
nos fijamos los hexágonos azul y turquesa son idénticos salvo el
tamaño, es decir
tienen la misma forma. En cambio, el hexágono verde no tiene la misma
forma. El hecho de tener la misma forma implica que existe una transformación llamada semejanza que transforma el uno en el otro. La semejanza conserva ángulos (forma) pero no distancias (tamaño). Por esta razón no se considera un movimiento en el plano. El lado del hexágono turquesa es el doble que el lado del hexágono azul. Por esta razón diremos que k=2 es la constante de semejanza. Los elementos que se corresponden en una semejanza se denominan homólogos. |
 |
1.- Indica todos los movimientos que conozcas en el plano.
2.- Calcula el cociente de las áreas de los hexágonos regulares: azul y turquesa. ¿Qué observas?
3.- ¿Cuál es el lado homólogo del hexágono turquesa correspondiente al lado ED del hexágono azul?
4.- ¿Cuál es el
ángulo homólogo del hexágono turquesa correspondiente al ángulo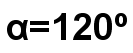 
del hexágono azul?
| Recuerda:
El área y características de un hexágono regular. |
Construcción
de figuras semejantes. Método de la proyección: Homotecia.
Dada una figura y un punto O desde el que deseamos proyectarla, trazaremos rectas que unan dicho punto O con la figura. Mediremos las distancias que hay desde O hasta los puntos A del contorno de la figura (en caso de ser poligonal elegiremos los vértices), a esas distancias las denominaremos OA.
Posteriormente, tomando la escala k que deseemos, calcularemos las distancias OA´=k*OA. Por último, situaremos el punto A´ sobre la recta trazada y haciendo lo mismo con todos los puntos de la figura inicial obtendremos su figura semejante.
La escala k, representa la razón de semejanza entre un punto A y su transformado (homólogo) A´, respecto al punto O que denominaremos centro. La transformación geométrica que transforma un objeto en otro semejante se denomina homotecia.
Por tanto,
denominaremos homotecia de centro O y
razón k (distinta de cero) a la transformación geométrica
definida anteriormente (OA´=k*OA con O, A y A´ alineados). De forma
que si k>0 se denomina homotecia directa y si k<0 homotecia inversa.
 |
 |
|
|||||||||||||||
Los contenidos de esta unidad
didáctica están bajo una licencia
de Creative Commons si no se indica lo contrario.
