|
Carlos
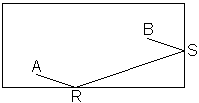
and Mr. John, his maths teacher, are playing a game of billiards. Soon
after they start Carlos asks Mr. John "what path would ball A have
to take to first bounce off two cushions before hitting ball B?"
(Problem
taken from the book "Matemáticas-Algoritmo
3" published by Vizmanos-Anzola Ed.SM - post-compulsory Secondary
education)
|
|
One
of the basic rules when solving problems is to start with the easy part first;
therefore, we shall first look at how the ball would bounce off "one"
of the cushions (the bottom one).
1.-
Move
point R along the cushion (use either the mouse or the numerical control buttons
underneath) until point S coincides with point B:
Now
we are going to look at how we get the solution both graphically and
analytically.
GRAPHICALLY
2.-
Copy
the billiards table and balls into your exercise book.
The
rectangle measurements are 28 x 14 "units".
Point
A is 7 u. from the left-hand cushion and 2 u. from the bottom cushion.
Point
B is 22 u. from the left-hand cushion and 5 u. from the bottom cushion.
|
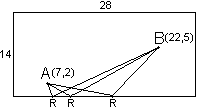 |
Point
R is the point where the distance between points A and B is the
shortest.
|
|
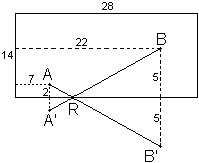
If
the bottom cushion didn't exist the ball would carry on until it got to
point B' (symmetrical to point B where
the bottom cushion is the line of symmetry), and
d(A,R)+ d(R,B) = d(A,R) + d(R,B') = d(A',R)+d(R,B)
is
at its shortest when points A, R and B' are in a straight line (as points
A', R and B would also be).
a)
Draw
point B'.
b) Draw line AB'.
c)
R is the point where line AB' intersects with the bottom cushion.
|
 |
ANALYTICALLY
First,
we set up a reference system with the origin in the lower
left-hand corner on the outside of the table. The bottom cushion represents the x-axis and
the left-hand cushion the y-axis. Thus, point A has the coordinates (7,2), point
B (22,5) and point B' (22,-5).
| 3.- a)
Work
out the equation of the line which passes through points A
and B'.
b)
Find
the point where this line cuts the x-axis.
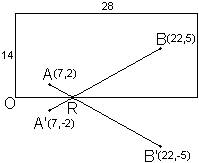
Sol: R = "7x+15y=79"  "y=0" = (79/7,0) "y=0" = (79/7,0) 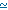 (11'286,0) (11'286,0) |
 |
(Note:
another exercise worth doing involves the same situation where the ball
bounces off one of the other three cushions)
|



