Para interpretar y extender las definiciones de las razones
trigonométricas a cualquier ángulo, y no únicamente a los triángulos
acutángulos4.1, se representan
las razones trigonométricas en una circunferencia de radio 1, a la
cual se denomina circunferencia goniométrica.
Figure 4.1:
Relación y representación de las razones trigonométricas
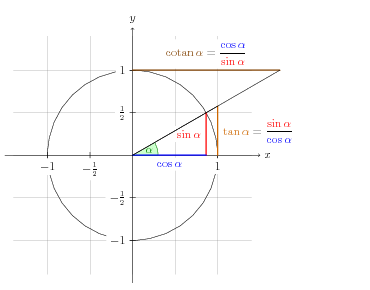 |
Es posible observar, entonces, que el seno de un ángulo corresponde
con la proyección sobre el eje 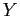 del radio, una vez colocado en el
ángulo adecuado respecto al eje
del radio, una vez colocado en el
ángulo adecuado respecto al eje 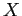 positivo. A su vez, el coseno del
ángulo corresponde con la proyección sobre el eje
positivo. A su vez, el coseno del
ángulo corresponde con la proyección sobre el eje  .
.
También se puede interpretar la tangente y la cotangente como se
indican en el gráfico. Las medidas de las proyecciones del radio se
pueden identificar con la medida de la prolongación del radio.
Se fácil representar, además, la
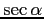 y la
y la
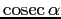 ,
pero como se superponen sobre el radio, se ha preferido dejar el
trabajo de su identificación al alumno.
,
pero como se superponen sobre el radio, se ha preferido dejar el
trabajo de su identificación al alumno.
Se considera más interesante que el alumno manipule estos elementos
por sı mismos, en lugar de una explicación textual. Por esto se
proponen el siguiente ejercicio:
Ejercicio 3
Utiliza el applet interactivo para realizar las siguientes
actividades:
- Utilizando los controles que puedes encontrar bajo el applet,
activa únicamente el seno y el coseno (poniendo los demás a
cero). Moviendo el punto de control sobre la circunferencia,
comprueba los valores que toman, respectivamente, el seno y el
coseno a medida que recorres con el punto de control la
circunferencia.
- Utilizando los controles que puedes encontrar bajo el applet,
activa únicamente la tangente y la secante (poniendo los demás a
cero). Moviendo el punto de control sobre la circunferencia,
comprueba los valores que toman, respectivamente, la tangente y la
secante a medida que recorres con el punto de control la
circunferencia.
- Utilizando los controles que puedes encontrar bajo el applet,
activa únicamente la cotangente y la cosecante (poniendo los demás
a cero). Moviendo el punto de control sobre la circunferencia,
comprueba los valores que toman, respectivamente, la tangente y la
secante a medida que recorres con el punto de control la
circunferencia.
- Ahora, para cada razón trigonométrica, lleva a cabo la
siguiente actividad: desactiva todas las razones (poniendo todos
los controles a cero) y moviendo el punto de control a lo largo de
la circunferencia, intenta adivinar cuanto valdrıa
(aproximadamente). Después lo compruebas activando la razón
correspondiente.
jmss
2009-05-07

![]() del radio, una vez colocado en el
ángulo adecuado respecto al eje
del radio, una vez colocado en el
ángulo adecuado respecto al eje ![]() positivo. A su vez, el coseno del
ángulo corresponde con la proyección sobre el eje
positivo. A su vez, el coseno del
ángulo corresponde con la proyección sobre el eje ![]() .
.
![]() y la
y la
![]() ,
pero como se superponen sobre el radio, se ha preferido dejar el
trabajo de su identificación al alumno.
,
pero como se superponen sobre el radio, se ha preferido dejar el
trabajo de su identificación al alumno.