
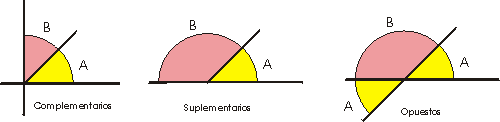
Ángulos complementarios, suplementarios y opuestos
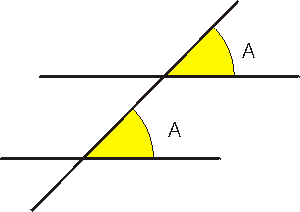
Ángulos de lados paralelos
Dos ángulos que tienen los lados paralelos son:
Suma de los ángulos de un triángulo
Si observamos la escena siguiente los tres ángulos con vértice en C y coloreados en rojo, amarillo y magenta son iguales respectivamente a A (ángulos de lados paralelos), C y B (ángulos de lados paralelos). De la figura se deduce que suman 180º.
Arrastra con el ratón los vértices A, B y C y comprueba cómo se mantiene igual a 180º la suma de los ángulos.
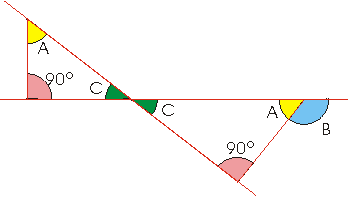
Ángulos de lados perpendiculares
Dos ángulos que tienen los lados perpendiculares son:
1. Mediatrices de un triángulo
Las mediatrices de un triángulo son las mediatrices de sus lados, es decir las perpendiculares a los lados trazadas por el punto medio de éstos. Los puntos de cada mediatriz están a la misma distancia de los extremos del lado sobre el cuál se ha trazado.
En la figura se observa claramente que las tres mediatrices se cortan en un único punto I. Este punto se denomina circuncentro. Según lo anterior se deduce que este punto está a la misma distancia de los tres vértices del triángulo. Se puede, por lo tanto, trazar una circunferencia con centro en dicho punto y que pase por los tres vértices. Esta circunferencia se denomina circunferencia circunscrita al triángulo.
Arrastra con el ratón los vértices A, B y C y comprueba cómo se desplaza el circuncentro y cómo cambia la circunferencia circunscrita cuando se modifican los vértices.
2. Alturas de un triángulo
Las alturas de un triángulo son las rectas perpendiculares a los lados que pasan por los vértices opuestos.
Si observamos la figura vemos que las tres alturas son también las mediatrices del triángulo A1, B1 y C1 (en azul), así pues se cortan en un punto que es el circuncentro de A1, B1 y C1. Este punto donde se cortan las alturas se denomina ortocentro del triángulo ABC.
Arrastrando los vértices A, B y C observa cómo se modifican las alturas y el ortocentro, observa también cómo cambia el triángulo A1B1C1.
3. Bisectrices
Las bisectrices de un triángulo son las bisectrices de sus ángulos. Las tres bisectrices se cortan en un punto que se denomina Incentro.
Se puede observar que la bisectriz tiene la propiedad de que sus puntos están a la misma distancia de los lados del ángulo al que divide. En consecuencia, el Incentro, al pertenecer a las tres bisectrices, está a la misma distancia de los tres lados del triángulo. Si trazamos un circunferencia con centro en este punto y radio la mencionada distancia observaremos que es tangente a los tres lados del triángulo. Esta circunferencia se denomina circunferencia inscrita.
Si prolongamos los lados del triángulo nos encontraremos en cada vértice con dos parejas de ángulos suplementarios. Consideremos también las bisectrices de los ángulos externos (que son perpendiculares a las correspondientes de los ángulos internos). Las bisectrices de dos angulos externos y del ángulo interno no adyacente se cortan y dan lugar a los puntos I1, I2 e I3 exteriores al triángulo ABC dado. Los puntos I1, I2 e I3 se denominan exincentros ya que son los centros de las circunferencias exinscritas al triángulo.
;
Arrastrando los vértices A, B y C podemos observar cómo se modifican las bisectrices y el incentro, así como los exincentros. También apreciaremos cómo cambian las circunferencias inscrita y exinscritas.
Nota: Si queremos una respuesta más rápida al movimiento de los controles podemos eliminar las rectas prolongación de los lados (configuración: eliminar todo el código en ecuaciones)
4. Medianas de un triángulo
Las medianas de un triángulo son las rectas que pasan por un vértice y el punto medio del lado opuesto.
Las tres medianas se cortan en un punto llamado baricentro. Sobre cada mediana el baricentro dista doble del vértice que del punto medio del lado. Cada mediana divide al triángulo en dos de igual área.
Arrastrando los vértices A, B y C observa cómo se modifican las medianas y el baricentro.
La escena siguiente puede utilizarse con distintas finalidades. Arrastrando los vértices y situándolos de forma adecuada podremos observar las relaciones entre los lados y ángulos del triángulo. Igualmente podremos comprobar el teorema de Pitágoras si hacemos que uno de los ángulos sea de 90º y observamos la relación entre los cuadrados de los lados .
Autor: Emilio Molina Avellaneda