VECTORS
Geometry
 
1. EQUIVALENT VECTORS

When we translate a shape on the plane we move it a certain quantity in a certain direction. Vector V is a single arrow which represents all the arrows indicating the magnitude and direction of each of the points of the shape being transformed. If we take one of these arrows, whose origin is at the origin of the axes, and go as far as the coordinates (x,y) at the end of the vector, we get a set of coordinates known as the vector coordinates.

All the arrows which are parallel to this one and go in the same direction are said to be equivalent (or equipollent) to the first arrow. We can see all the arrows associated with the vector (Vx,Vy) in the following Descartes window. The coordinates of the origin and end point of the respective arrows are different but the vector coordinates are always the same.

 
1.- Drag the origin of the vector with the mouse and move it around the window.

2.- Draw the vector (-3,-2) in your exercise book and draw four equivalent vectors with their origins in each of the four quadrants.

3.- Do the same thing for the following vectors (4,-3), (-5,3) and (5,2).

Click on the Init button and move the origin of the vector to (-3,2). Note that we obtain the vector coordinates by taking away the origin coordinates from those of the end point of the vector, i.e. Vx=-1-(-3)=2; Vy=5-(2)=3. Change the position of the origin and check that the relation is satisfied.
4.- Draw a vector in your exercise book whose origin is (1,0) and end point (-4,1) and work out its coordinates. Check your answer in the Descartes window by first putting in the coordinates and then by moving the vector until it coincides with the two given points.
2. THE COORDINATES OF A VECTOR

Use the Descartes window on the left to help you work out vector coordinates. Random vectors appear each time you click on the Init button. 
5.- Copy the vector which appears in the left-hand window into your exercise book and work out its coordinates. Check your results afterwards in the window on the right by moving the vector origin to the point where it is found and put in coordinates until you find those of an equivalent vector. Every time you click on the Init button a new vector appears. Repeat the exercise at least 10 times.
3. ADDING VECTORS

The sum of the given vectors U and V is known as vector S, whose coordinates are the sum of the coordinates of the other two vectors.

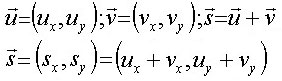To get different vectors drag the red points with the mouse or write its coordinates on the line underneath.

6.- Work out the sum of the vectors U=(5,2) and V=(1,3). Find the coordinates of the sum vector and draw it in your exercise book. Compare the results you get with those given on the Descartes window.

7.- Repeat the exercise with the following vectors: U=(-2,3) and V=(2,-3).

8.- Two vectors are opposite if their sum is the vector (0,0). What are the coordinates of the vector opposite the vector U=(2,-3)?

9.- What is the connection between the coordinates of a vector and its opposite vector?
       
           
  Miguel García Reyes
 
Spanish Ministry of Education. Year 2001
 
 

Licencia de Creative Commons
Except where otherwise noted, this work is licensed under a Creative Common License