
 |
ANGLEs IN A polYGOn |
| Geometry | |
| 1. interior AND EXTERIOR ANGLES | |
| There
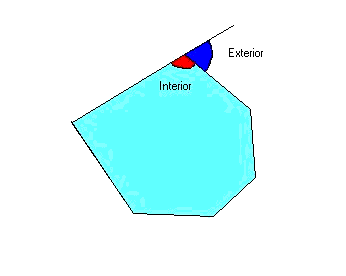
are two types of angle in a polygon: interior and exterior.
The interior angle is the angle formed between two adjacent sides and the
exterior angle is the supplementary angle.
We know that the sum of the interior angles in any triangle is 180º. As any polygon can be divided into triangles we can use this technique to work out the sum of the angles inside a polygon. A
quadrilateral can be divided into 2 triangles, a pentagon into 3, a
hexagon into 4 etc. The amount of triangles that the polygon can be
divided into is always 2 less than the total number of sides i.e. a
polygon with n sides can be divided into n-2 triangles.
Therefore, the sum of the interior angles is 180º·(n-2).
In a regular polygon the value of one of the interior angle is:
In any polygon the exterior angles add up to 360º. If we consider that an interior and exterior angle add up to 180º, the sum of all the angles in an n-sided polygon would be n·180º. As the interior angles add up to 180º·(n-2) the difference is 360º. |
 |
| 1.- You
can see how each exterior angle of the triangle is the same as the next
and how the three together make a complete revolution. The same thing happens
with the four exterior angles of a square, the five of a pentagon etc.
2.- Increase the number of sides of the polygon and watch how the exterior angles become smaller in size. Notice how, at the same time, the interior angles get larger. 3.- Work out the values of the interior and exterior angles of 20 and 40-sided regular polygons. Check your results in the Descartes window. 4.- Draw some irregular polygons in your exercise book. Label the exterior angles and check that the above is true in these cases too.
|
|
| 2. The central angle in a regular polygon | |||
| If we imagine a regular polygon inscribed in a circle, the central angle is formed by two consecutive radii of the polygon. All the central angles add up to 360º, as do the exterior angles. | |||
5.- Work
out the size of the
central angle of a 6, 12, 20 and 36-sided polygon. Check your results
in the window.
|
|||
| Miguel García Reyes | ||
 |
||
| Spanish Ministry of Education. Year 2001 | ||

Except where otherwise noted, this work is licensed under a Creative Common License