
Propiedades operativas de los límites en un punto.
 |
Propiedades de los límites: Propiedades operativas de los límites en un punto. |
| Análisis. | |
| Introducción. | |
|
En este capítulo vamos a estudiar las propiedades de los límites en relación con las operaciones aritméticas básicas. Estas propiedades son muy importantes para encontrar métodos sencillos y prácticos de cálculo de límites. | |
| Límite de una suma de funciones. | |
|
"Sean f y g dos funciones con límite en el punto a, respectivamente b y c. Entonces la función f+g también tiene límite en el punto a y vale b+c".
Es decir
|
|
Manipula la gráfica lo necesario para contestar a las preguntas que se plantean a continuación.
| ||
|
1.- Selecciona un valor para e. Ampliando la imagen si fuera preciso averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad f(x) dista de b menos que e/2. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
2.- Con el mismo valor de e que en el apartado anterior averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad g(x) dista de c menos que e/2. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
3.- Haz ahora que d tome el valor más pequeño de los dos que has obtenido y contesta a la siguiente cuestión. Si x está dentro del intervalo limitado por las rectas verticales azules ¿qué puede afirmarse de la distancia entre (f+g)(x) y b+c? | ||
|
4.- ¿Puede afirmarse lo mismo si hago que e tome cualquier otro valor? | ||
|
Observa ahora la siguiente desigualdad:
Si has contestado satisfactoriamente a las preguntas anteriores habrás obtenido que sea cual sea el valor de e (mayor que cero) es posible encontrar otro número positivo d tal que si la distancia entre x y a es menor que d, entonces la distancia entre f(x) y b es menor que e/2 y la distancia entre g(x) y c también, por lo tanto la distancia entre (f+g)(x) y b+c es menor que e. | ||
| Límite de un producto de funciones. | |
|
"Sean f y g dos funciones con límite en el punto a, respectivamente b y c. Entonces la función fg también tiene límite en el punto a y vale bc".
Es decir
|
|
Manipula la gráfica lo necesario para contestar a las preguntas que se plantean a continuación.
| ||
|
1.- Selecciona un valor para e. Ampliando la imagen si fuera preciso averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad g(x) está acotada por cierto valor m (en nuestro caso debes suponer m=3). Anota el valor de d obtenido. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
2.- Con el mismo valor de e. Ampliando la imagen si fuera preciso averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad f(x) dista de b menos que e/2m, siendo m el valor del apartado anterior. Anota el valor de d obtenido. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
3.- Con el mismo valor de e que en el apartado anterior averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad g(x) dista de c menos que e/2b. Anota el valor de d obtenido. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
4.- Haz ahora que d tome el valor más pequeño de los tres que has obtenido y contesta a la siguiente cuestión. Si x está dentro del intervalo limitado por las rectas verticales azules ¿qué puede afirmarse de la distancia entre (fg)(x) y bc? | ||
|
5.- ¿Puede afirmarse lo mismo si hago que e tome cualquier otro valor? | ||
|
Observa ahora la siguiente cadena de desigualdades:
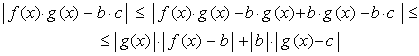
Si has contestado satisfactoriamente a las preguntas anteriores habrás obtenido que sea cual sea el valor de e (mayor que cero) es posible encontrar otro número positivo d tal que si la distancia entre x y a es menor que d, entonces, |g(x)| es menor que m, la distancia entre f(x) y b es menor que e/2m y la distancia entre g(x) y c es menor que e/2b. Por lo tanto, la distancia entre (fg)(x) y bc es menor que e. | ||
| Límite de la inversa de una función. | |
|
"Sea f(x) una función con límite en el punto a, igual a b y b distinto de cero. Entonces la función 1/f(x) también tiene límite en el punto a y vale 1/b".
Es decir
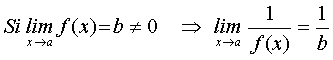
|
|
Manipula la gráfica lo necesario para contestar a las preguntas que se plantean a continuación.
| ||
|
1.- Modifica el valor de m hasta conseguir una cota inferior de f(x) que sea positiva. Una vez conseguido, halla algún valor d para el que si x dista de a menos que d f(x) es mayor que m con toda seguridad. Anota el valor de d obtenido. ¿Es siempre posible hallar un tal valor de m por muy pequeño que sea b? Razona la respuesta. | ||
|
2.- Selecciona un valor de e. Ampliando la imagen si fuera preciso averigua para qué valor de d se cumple que si x dista de a menos que d con toda seguridad f(x) dista de b menos que bme, siendo m el valor del apartado anterior. Anota el valor de d obtenido. ¿Es siempre posible encontrar un valor d que cumpla esta condición? ¿Por qué? | ||
|
3.- Haz ahora que d tome el valor más pequeño de los dos que has obtenido y contesta a la siguiente cuestión. Si x está dentro del intervalo limitado por las rectas verticales azules ¿qué puede afirmarse de la distancia entre 1/f(x) y 1/b? | ||
|
4.- ¿Puede afirmarse lo mismo si hago que e tome cualquier otro valor? | ||
|
Observa ahora la siguiente cadena de desigualdades:
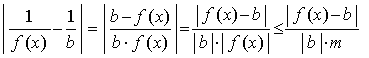
Siendo m una cota inferior positiva de f(x).
Si has contestado satisfactoriamente a las preguntas anteriores habrás obtenido que sea cual sea el valor de e (mayor que cero) es posible encontrar otro número positivo d tal que si la distancia entre x y a es menor que d, entonces, |f(x)| es mayor que m>0 y la distancia entre f(x) y b es menor que |b|me. Por lo tanto, la distancia entre 1/f(x) y 1/b es menor que e. | ||
| Límite de una función constante. | |
|
"Sea f(x)=k una función constante. El límite de f(x) en el punto a es k".
Es decir
|
|
Haz que x se aproxime al punto a. ¿A quién se aproxima f(x)? |
| Límite de la función identidad. | |
|
"Se considera la función identidad: f(x)=x. El límite de f(x) en el punto a es a".
Es decir
|
|
Haz que x se aproxime al punto a. ¿A quién se aproxima f(x)? | |
| Consecuencias
Las siguientes afirmaciones son consecuencia directa de las propiedades anteriores. Demuéstralas como ejercicio:
|
| José Luis Alonso Borrego | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||
![]()
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.